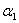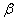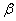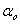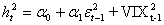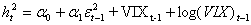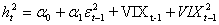La procedura di stima parte sempre da modelli più semplici consideranto il numero più basso di ritardi: si inizia dal modello ARCH(1) per poi stimare un GARCH(1,1) e un TGARCH(1,1), inserendo le variabili VIXt-1, log(VIX)t-1 e VIX2t-1 come segue:
ARCH(1)+ VIXt-1 ARCH(1)+ log(VIX)t-1 ARCH(1)+ VIX2t-1 ARCH(1)+ VIXt-1+ log(VIX)t-1 ARCH(1)+ VIXt-1+ VIX2t-1
GARCH(1,1)+ VIXt-1 GARCH(1,1)+ log(VIX)t-1 GARCH(1,1)+ VIX2t-1 GARCH(1,1)+ VIXt-1+ log(VIX)t-1 GARCH(1,1)+ VIXt-1+ VIX2t-1
TGARCH(1,1)+ VIXt-1 TGARCH(1,1)+ log(VIX)t-1 TGARCH(1,1)+ VIX2t-1 TGARCH(1,1)+ VIXt-1+ log(VIX)t-1
TGARCH(1,1)+ VIXt-1+ VIX2t-1
Per testare la significatività dei modelli si utilizzano 3 informazioni di stima:
1- La probabilità dei coefficienti: per ogni variabile inserita nel modello (sia endogena che esogena) l’output di stima calcola un peso, o coefficiente, attribuito ad ogni variabile, allo stesso tempo ad ogni coefficiente è associata una probabilità che informa se il vaole stimato è accettato oppure no. Con una probabilità maggiore del 5% (P>0,05) non si accetta la significatività dei coefficienti stimati dal modello, al contratio se questa probabilità è minore del 5% i coefficienti stimati sono accettati dal modello.
2-Test per valutare l’ipotesi nulla di omoschedasticità della componente stocastica (test ARCH LM, Engle 1982). Si assume di avere eteroschedasticità nei residui, distribuiti come un autoregressivo di ordine p:
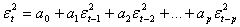
in modo che la dimensione dei residui correnti, al quadrato, è collegata a quella dei residui passati. La particolare specificazione scelta per l’eteroschedasticità è motivata dall’osservazione che per dati economici molto spesso la dimensione dei residui correnti appare correlata con la dimensione dei residui più recenti. Una volta specificato il valore p per valutare l’ipotesi di omoschedasticità:
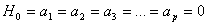
si considera la regressione di 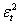 sui suoi ritardi e si determina la statistica test LM=TR2, che si distribuisce come un
sui suoi ritardi e si determina la statistica test LM=TR2, che si distribuisce come un 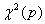 . Anche in questo caso con probabilità maggiore del 5% non rifiuto l’ipotesi nulla.
. Anche in questo caso con probabilità maggiore del 5% non rifiuto l’ipotesi nulla.
3-Correlogrammi della statistica Q di Ljung e Box:
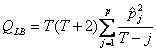
Dove 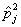 è la j-esima autocorrelazione, T il numero di osservazioni.
La statistica
è la j-esima autocorrelazione, T il numero di osservazioni.
La statistica 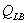 è utilizzata per valutare che, nella serie degli errori della stima del modello, tutte le
è utilizzata per valutare che, nella serie degli errori della stima del modello, tutte le 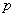 autocorrelazioni siano nulle. L’ipotesi nulla è quindi che
autocorrelazioni siano nulle. L’ipotesi nulla è quindi che 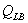 si distribuisca come un
si distribuisca come un 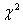 con
con 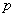 gradi di libertà, quindi tale ipotesi non è accettata con una probabilità maggiore del 5%, in questo caso si può affermare che non vi è più correlazione fra i residui.
gradi di libertà, quindi tale ipotesi non è accettata con una probabilità maggiore del 5%, in questo caso si può affermare che non vi è più correlazione fra i residui.
Se tutte queste condizioni vengono soddisfatte si può ritenere di aver stimato un buon modello.
Modello ARCH(1)à 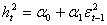
MODELLO |
VARIABILI ESOGENE |
SIGNIFICATIVITA’ COEFFICIENTI |
H0 DI OMOSCHEDASTICITA’ |
RESIDUI INCORRELATI |
||
ARCH(1) |
VIXt-1 |
Non accettata
|
Accetta H0
|
INCORRELATI |
||
ARCH(1) |
log(VIX)t-1 |
ACCETTATI |
Accetta H0
|
CORRELATI |
||
ARCH(1) |
VIX2t-1 |
ACCETTATI |
Accetta H0
|
INCORRELATI |
||
ARCH(1) |
VIXt-1 log(VIX)t-1 |
ACCETTATI |
Accetta H0
|
INCORRELATI |
||
ARCH(1) |
VIXt-1 VIX2t-1 |
ACCETTATI |
Accetta H0
|
INCORRELATI |
Figura 32: Significatività modello ARCH(1)
Modello GARCH(1,1)à 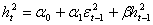
MODELLO |
VARIABILI ESOGENE |
SIGNIFICATIVITA’ COEFFICIENTI |
H0 DI OMOSCHEDASTICITA’ |
RESIDUI INCORRELATI |
||
GARCH(1,1) |
VIXt-1 |
ACCETTATI |
Rifiuta H0
|
INCORRELATI |
||
GARCH(1,1) |
log(VIX)t-1 |
ACCETTATI |
Rifiuta H0
|
INCORRELATI |
||
GARCH(1,1) |
VIX2t-1 |
Non accettata
|
Accetta H0
|
INCORRELATI |
||
GARCH(1,1) |
VIXt-1 log(VIX)t-1 |
ACCETTATI |
Rifiuta H0
|
INCORRELATI |
||
GARCH(1,1) |
VIXt-1 VIX2t-1 |
Non accettata
|
Accetta H0
|
INCORRELATI |
Figura 33: Significatività modello GARCH(1,1)
Modello TGARCH(1,1) à 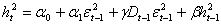
MODELLO |
VARIABILI ESOGENE |
SIGNIFICATIVITA’ COEFFICIENTI |
H0 DI OMOSCHEDASTICITA’ |
RESIDUI INCORRELATI |
||
TGARCH(1,1) |
VIXt-1 |
ACCETTATI |
Rifiuta H0
|
INCORRELATI |
||
TGARCH(1,1) |
log(VIX)t-1 |
ACCETTATI |
Rifiuta H0
|
INCORRELATI |
||
TGARCH(1,1) |
VIX2t-1 |
Non accettata
|
Rifiuta H0
|
INCORRELATI |
||
TGARCH(1,1) |
VIXt-1 log(VIX)t-1 |
ACCETTATI |
Rifiuta H0
|
INCORRELATI |
||
TGARCH(1,1) |
VIXt-1 VIX2t-1 |
ACCETTATI |
Rifiuta H0
|
INCORRELATI |
Figura 34: Significatività modello TGARCH(1,1)
Dalle stime dei modelli solamente 3 rispettano tutte le condizioni di significatività:
Per verificare quale di questi modelli è il migliore è opportuno osservare il loro punteggio AIC (Akaike info criterion):
MODELLO |
AIC |
|
ARCH(1)+ VIXt-1+ VIX2t-1 |
|
|
ARCH(1)+ VIX2t-1 |
|
|
ARCH(1)+ VIXt-1+ log(VIX)t-1 |
|
Figura 35: Modelli con migliore punteggio AIC
Sono stati stimati altri modelli aumentando il numero di ritardi: ARCH(2), GARCH(2,1), TGARCH(2,1), GARCH(2,2) e TGARCH(2,2), ma nessuno di questi accettava le 3 condizioni di significatività contemporaneamente, inoltre è sempre opportuno scegliere specificazioni più semplici del modello.
Successivo: 3.5.3 Effetto VIX e VIX2 Congiunto
Sommario: Index