Riscontri dall’analisi “Level AR”

Come è stato visto precedentemente il VR è un valido strumento per rilevare gli allontanamenti dalla random walk, ma questo strumento identificativo, non ha anche caratteristiche predittive, così recentemente Kandel e Zilca (2001) hanno presentato in un loro articolo, un modello di regressione che può essere espresso come funzione del variance ratio.

Il modello Level auto-regression (LAR) ha l’importante caratteristica d’essere la sola possibile rappresentazione regressiva del VR, dal momento che entrambi gli strumenti sono rappresentabili in termini di autocorrelazione con pesi linearmente decrescenti. La non stazionarietà delle serie di prezzi, che implica una deriva (drift) diversa da zero, non rende, infatti, possibile la regressione di un vettore dei rendimenti stimati sui prezzi ritardati.

L’equazione di auto-regressione ha la seguente forma:

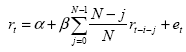(9.7.5)

in cui r_t rappresenta la differenza logaritmica (dunque il rapporto) tra p _t e p _t-1 e il coefficiente ß moltiplica la statistica LAR ritardata di i, che a sua volta riprende la lagged form del VR espressa nella (9.7.3). Questa statistica è in grado di rivelare alcuni indicativi comportamenti delle serie storiche finanziarie, tra cui la persistenza di breve periodo (il momentum) di una tendenza, e la Mean-Reversion nel lungo periodo. Inoltre tale strumento conferma la presenza di volatility clustering nelle serie di prezzi.

Mean Reversion nelle commodities

Argomentazioni interessanti sono piuttosto quelle che giungono da Bessembinder, Coughenour, Seguin e Smoller (1995), i quali attraverso lo studio della struttura a termine dei prezzi futures tentano di capire se gli investitori anticipano la mean reversion dei prezzi spot. La loro indagine rileva (come altri test hanno fatto successivamente) che sono soggetti alla mean reversion in particolare le commodities legate all’agricoltura ed il greggio.

Per quest’ultimo è stato rilevato che il 44 percento di uno shock sul prezzo spot è destinato a regredire verso la media negli otto mesi successivi. Anche per i metalli sembra valere questo comportamento, sebbene in misura più contenuta. In ogni modo sembra che il processo stocastico di mean reversion sia particolarmente adatto alle commodities: anche la microeconomia sostiene che nel lungo periodo il prezzo di una commodity dovrebbe essere legato al suo costo marginale di lungo periodo, o nel caso di cartelli come il petrolio, al prezzo che massimizza i profitti di lungo periodo.

Infatti sebbene il prezzo del petrolio oscilli in modo sensibile nel breve periodo, nel lungo tende al suo valore normale di equilibrio.

Mean Reversion with Jumps: il caso del Brent[94]

Per il petrolio, come pure per altre commodities sembra che si lavori meglio con processi “Poisson-Gaussiani”, chiamati processi di diffusione a salti, che combinano il processo di Itô con un processo di Poisson (e quindi mischiano il continuo col discreto), ed ha una forma del tipo:

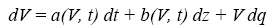(9.7.5)

in cui i primi termini sono come quelli visti in precedenza, ma dq è il termine di Poisson definito in modo che:

dq = 0, con probabilità 1- λdt

dq = Φ - 1, con probabilità λdt

in cui dz (il processo di Wiener) e dq sono indipendenti tra loro, λ è la frequenza dei salti e Φ è la distribuzione di probabilità della misura del salto, così che in caso di salto la variabile V diventerà VΦ. Il modello di diffusione a salti prevede che il prezzo sia legato all’arrivo d’informazione.

Nel prezzo del petrolio tuttavia, come per altri asset esistono notizie normali che comportano variazioni “smooth”, e notizie anormali che fanno saltare i prezzi. Il primo tipo di variazione segue un processo (continuo) di mean reversion, mentre i salti seguono un processo di Poisson (discreto), in cui gli intervalli tra i salti sono variabili esponenziali IID. Secondo questo modello si suppone che il prezzo del petrolio segua il seguente processo geometrico mean-reverting con salti:

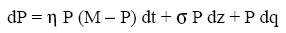(9.7.6)

in cui il termine di Poisson dq vale zero fin quando con frequenza λ assume un valore che fa spiccare un salto alla variabile sottostante. Com’è stato detto poco sopra i processi di Wiener e di Poisson sono non correlati e la distribuzione di probabilità della dimensione del salto è data da Φ, di modo che, dato un salto, il suo valore atteso è k = E[Φ - 1].

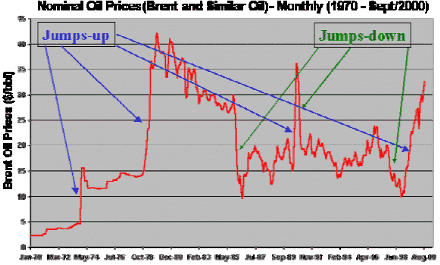
Figura 27. Fonte www.puc-rio.br/marco.ind

Nella figura 27, sono stati evidenziati nell’andamento del prezzo del Brent i salti di cui si è parlato, i quali sembrano nel lungo periodo inserirsi in un processo mean-reverting coerente con il modello formale sopra esposto.

94 Questo paragrafo è stato realizzato grazie all’aiuto ed al materiale resomi disponibile dall’ ingegnere petrolifero Marco Antonio G. Dias, il quale ha organizzato presso il sito dell’Università Pontificia Cattolica di Rio de Janeiro, il suo website personale dedicato alle opzioni reali nel petrolio.

Marco Primavera

Successivo: Strategie per battere il mercato: "contrarian" e "momentum"

Sommario: Index