We start with a formal definition of our process which we use the rest of the thesis. An N-dimensional Ito SDE with an M-dimensional Wiener process, e.g. with M pair-wise independent scalar Wiener processes 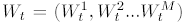as its components, will be written in vector form as:

or more general, as a component-wise:

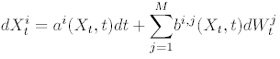(3)

This vector SDE could thus be written as:

dXt = A(Xt, t)dt + B(Xt, t)dWt

Similar notation can be used for a Stratonovich SDE:

dXt = A(Xt, t)dt + B(Xt, t) ◦ dWt

Ito Stochastic Calculus

For a sufficiently smooth transformation U : [0, T ] × RN --> R of the solution Xt of the Ito {SDE-3}:

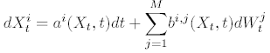
f or i = 1, ..., N ; j = 1, ..., M

the scalar process Yt = U (Xt, t) satisfies the following Ito SDE:

(4)

with the differential operators L⁰, L¹, :::, L^M with respect to this SDE:

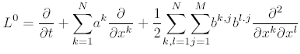
and

These operators play a fundamental role in Ito stochastic calculus through the Ito formulae for the stochastic chain rule and subsequently for stochastic Taylor expansions and numerical schemes for the SDEs that are based on stochastic Taylor expansions. It differs from what might be expected from deterministic calculus by the presence of the second order term in the L⁰ operator, which is essentially due to the fact that E((W )²) = Δt for the increment of a Wiener process over an interval of length Δt.

Stratonovich Stochastic Calculus

For a sufficiently smooth transformation U : [0, T ] × RN --> R of the solution Xt of the Stratonovich SDE:

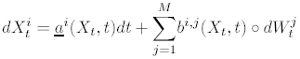(5)

f or i = 1, ..., N ; j = 1, ..., M

the scalar process Yt = U (Xt, t) satisfies the following Stratonovich SDE:

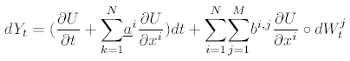(6)

where the terms are all evaluated at (Xt, t). In operator form, this is:

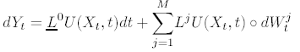
The L⁰ operator of Ito calculus needs to be changed in Stratonovich calculus to:

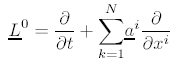
while the Lj operators of Ito calculus remain unchanged in Stratonovich calculus.

Prof. Klaus Schmitz

Next: Ito-Stratonovich drift conversion

Summary: Index