Using the following trick:

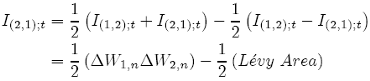(29)

we obtain the equation to calculate the double integral using Lévy Area. Now, to measure this area, we can integrate:

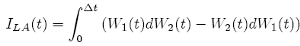
Then the Fourier transformation of the density of ILA conditional on ∆W1, ∆W2 is given by:

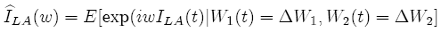
and is explicitly known by [5] (it is also given in Lévy’s original paper [10]) as:

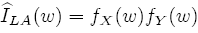
where, given R2 = (∆W₁)² + (∆W₂)²:

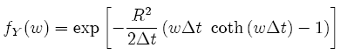
The probability density function (pdf) for X can be obtained exactly by inverting the Fourier transform fX (w):

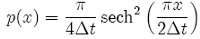
and then the cumulative distribution function (cdf) is:

leading, via its inverse, to the sample rule:

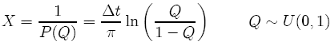(30)

Note that the variance of X is:

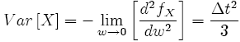
So far as we know, the pdf for Y cannot be written down in exact form, but for small ∆t, we have:

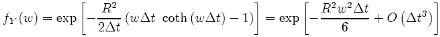
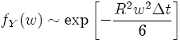(31)

which is the Fourier transform of another normal distribution with density:

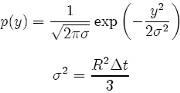
Samples of Y can then be made in the usual way.

(32)

So the double integral {24} can be approximated using the formulae:

(33)

We explicitly know that the total variance of the Lévy Area is:

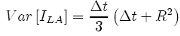
So, although {33} is an approximation, we can see that we recover the exact total variance required.

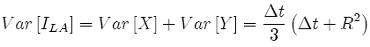
Prof. Klaus Schmitz

Next: Exact Fourier Lévy formulae

Summary: Index