Suppose that we can find the solution of the PDE, say G(w, ν, τ ), with the property that at t = T , G(w, ν, 0) = 1. Then the solution to the transformed PDE {48} with payoff condition U (w, ν, 0) is just the product of this with G.

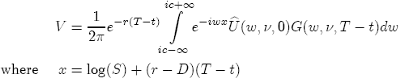(49)

Lewis (refer to [11]) discusses how to solve {49} for the general case, but here we will only solve for the Heston model (γ = 1/ 2 ).

Greeks for free

Before figuring out G, we should point out that {49} is a remarkably useful representation. If you want to differentiate V with respect to S to obtain ∆, you merely multiply the integral by:

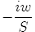
and for Γ, the integral is multiplied by:

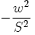
This representation also makes obvious the link between ρ and ∆.

Finding the fundamental solution

For γ = 1/ 2 and Heston parameters, the PDE {48} yield the form:

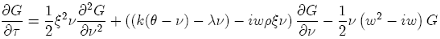(50)

What Heston [6] does is try to find a solution in the form:

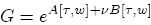
with:

A [0, w] = B [0, w] = 0

in order to satisfy the condition that G[0, w] = 1 (at maturity). If we substitute this assumption for the form of G into the PDE {50}, we obtain the following condition:

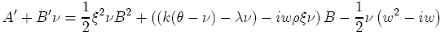
The A' and B' denote the τ − derivative. This must be true for all ν so we separately equate the terms that are independent of ν and linear in ν to obtain the pair of ordinary differential equations:

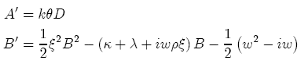
Solving this, we obtain:

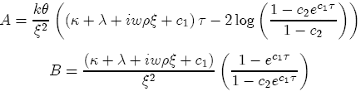
where:

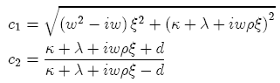
So the exact solution of the option price using Heston volatility is:

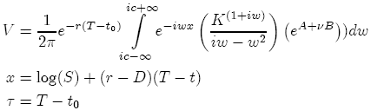(51)

using the condition:

for

Call options Im(w) > 1

Put options Im(w) < 0

For further information or more details, see [16] or [6].

Prof. Klaus Schmitz

Next: Derivation of the 2D Milstein Scheme

Summary: Index