In the Fourier method described above, we use uniform and normal independent random numbers (Q & Z) to calculate the samples of X and Y. However, if we assume the opposite, that Q and Z are functions of the original random numbers that create the Wiener process Wi:
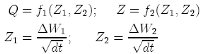(34)
and using exactly the same criteria of the Fourier Lévy formulae described above (page 16), we get a better approximation to calculate the probability for our double integral {24}:
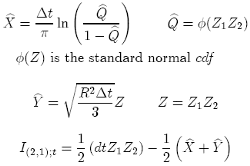(35)(36)(37)
Because the equation {35} can not be defined at some point, we replace it with the following:
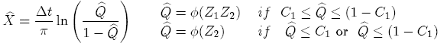(38)
where C1 is a constant to avoid having division or logarithm of zero or close to it.
The assumption {34} is strong, but as well the results in the simulations. The use of {37} to calculate the double integral gives us a better and more stable approximation for all time steps n than the simple Fourier formulae shown in {33}. Furthermore, if we use only Z1 or Z2 and/or the combination with other independent random numbers, the numerical results are never as good as using the original formulae {33}. All these strong conclusions convince us that {37} is the best combination and, therefore, is called the Exact Fourier Lévy formulae.
Prof. Klaus Schmitz
Next: Real Variance formulae
Summary: Index