General 2D Milstein scheme for stochastic volatility models

The {SDE-19} is the 2D Milstein approximation for the following SDEs:

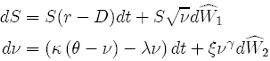
However, if we try to be more general with respect to the drift of the variance, we need to represent it with a function with respect to "ν":

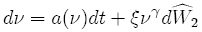
Using this equation and the definition in {10}, we arrive to the General 2D Milstein scheme for stochastic volatility models:

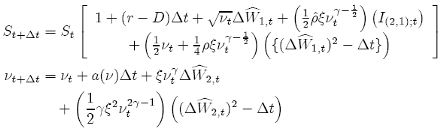(22)

where a(ν) can be any volatility drift term. We can see that {22} is very similar to {21} and this is because the Milstein scheme and its Ito operators use only the noise intensity term in their transformations.

The approximation {22} is very useful, because it is the general representation for all famous stochastic volatility models that appear in the literature [12]. For example, if we use:

a(ν) = (w − ζ ln(ν))

and γ = 0, we arrive to the 2D Milstein scheme for the stochastic model proposed by Scott in 1989.

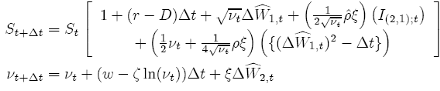(23)

Prof. Klaus Schmitz

Next: Approximations of the Double Integral

Summary: Index