In this section, we present five methods of how we can simulate the double integrals {24} for the 2D Milstein approximation {19}.

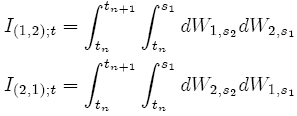(24)

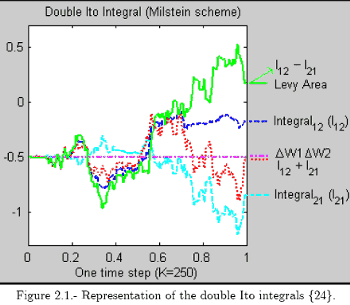
These double integrals, as we see in figure 2.1, start at zero, and then each one follows its own random path. At the end of the time step, the sum of both integrals is ∆W1∆W2 and the difference between both is what is called Levy Area. This is a very important concept in stochastic calculus.

Levy Area = I_(1,2);t − I_(1,2);t

We start with the subdivision method proposed by Kloeden [9]. We follow with the problems of using this method, and we propose a solution. We continue with two explicit Fourier formulas and with a method using the real mean and variance of the integral. The last method is a summary of all and gives the best approximation. Simulations and conclusions are given at the end, and we compare all of them with an explicit formulae for the Heston model.

Subdivision (Kloeden)

Kloeden in [9] says that the double integral {24} can be approximated by applying the (vector valued) stochastic Euler scheme to the 2 dimensional (2D) Ito SDE:

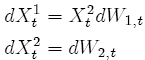(25)

over the discretization subinterval [tn, tn+1] with a suitable size:

δ = (tn+1 − tn) /NK

The solution of the {SDE-25}, with the initial conditions:

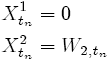(26)

and at time t = tn+1, is given by:

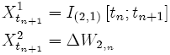
Using t'k = tn + kδ and δ_Wj,n,k = W_j,t'k+1 − W_j,t'k , the stochastic Euler scheme for the {SDE-25} is:

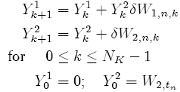
and when k = NK − 1, we obtain the solution of the double integral {24}:

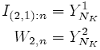
and other important variables for the process:

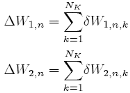
Kloeden in [9] says that the strong order of convergence of γ = 1 2 of the stochastic Euler scheme ensures that:

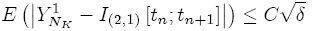
Therefore, I_(2,1) [tn; tn+1] can be approximated in the Milstein scheme by

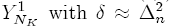without affecting the overall order of convergence. Other higher order multiple stochastic integrals can be simulated in a similar way.

Prof. Klaus Schmitz

Next: Subdivision (Kloeden - IC = 0)

Summary: Index