Following Einstein’s explanation of physically observed Brownian motion during the first decade of the 1900s, the physicists Langevin, Smoluchowski, and others attempted to model the dynamics of such motion in terms of differential equations. Instead of a deterministic ordinary differential equation:

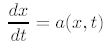
they obtained a noisy differential equation of the form:

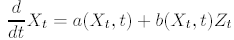
with a deterministic or averaged drift term a(Xt, t) perturbed by a noise intensity term b(Xt, t)Zt, where the Zt are independent N(0, t)−distributed Gaussian random variables for each t and b(Xt, t) is an intensity factor that will, in general, depend on both the t and X variables. The driving process Zt, which is called Gaussian white noise, appears formally to be the path-wise derivative of a mathematical Brownian motion or Wiener process Wt, a Gaussian process with W0 = 0 and N(0, t)−distributed for each Wt, e.g.. with:

E (Wt) = 0

E ((Wt)²)= t

(1)

which has independent increments:

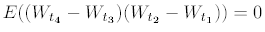
for all 0 ≤ t1 ≤ t2 ≤ t3 ≤ t4.

However, the Gaussian white noise process is not a conventional process, having, for example, covariance equal to a constant multiple of the Dirac delta function. Moreover, it is now known that the sample paths of a Wiener process Wt are nowhere differentiable. This suggests that the stochastic differential equation one {SDE-1}, which might be written symbolically in terms of differentials as:

dXt = a(Xt, t)dt + b(Xt, t)dWt

(2)

should be interpreted in some sense as an integral equation:

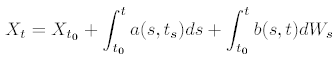
The first integral here is just path-wise an ordinary Riemann integral. While it might seem that the second integral could be a Riemann-Stieltjes integral for each sample path, this is not possible because the sample paths of a Wiener process are not just not differentiable, but also are not even of bounded variation on any bounded time interval. In the 1940s, the Japanese mathematician K. Ito proposed a means to overcome this difficulty with the definition of a new type of integral, a stochastic integral, which is now called an Ito stochastic integral. Later, in the 1960s, the Russian physicist R. L. Stratonovich proposed another kind of stochastic integral, now called the Stratonovich stochastic integral, which is distinguished from the Ito integral by a “◦" before the differential dWs, e.g. written symbolically in the differential form:

dXt = a(Xt, t)dt + b(Xt, t) ◦ dWt

but really an integral equation:

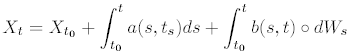
There are thus two types of stochastic calculus, the Ito stochastic calculus and the Stratonovich stochastic calculus, depending on the type of stochastic integral used. Both have their advantages as well as their disadvantages. Which one should be used is more a modelling than mathematical issue, but once one has been chosen, a corresponding equation of the other type with the same solutions can be determined. Therefore, it is possible to switch between the two stochastic calculi.

Prof. Klaus Schmitz

Next: Ito and Stratonovich Stochastic Calculus

Summary: Index