The "General Heston Model" is:
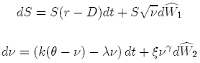
We abbreviate the second of these in the form:
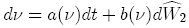
In doing so, we arrive to the General PDE for stochastic volatility:
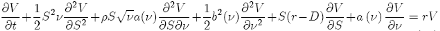 (46)
(46)
We can see that the last PDE {46} and the original Black-Scholes PDE have a lot of similarity. Applying a similar set of transformations and using T equal to the maturity of the contract:
τ = T − t
x = log(S) + (r − D)(T − t)
V = U (x, ν, τ )e−r(T −t)
and after some routine calculus using the chain rule, leads to a PDE for "U" in the form:
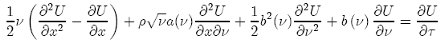
Now, if we introduce the Fourier transform in the following form:
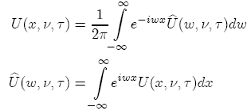 (47)
(47)
then at maturity, where τ = T − t = 0, we have:
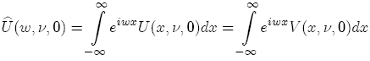
which is the Fourier Transform of the payoff expressed in terms of the logarithm of the asset price. So the differentiation w.r.t. "x" is equal to the multiplication by (−iw) in the transform:
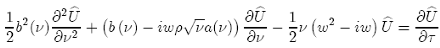 (48)
(48)
European option
The payoff of a call European option is max[S −K, 0] in terms of our original variables. In terms of logarithmic variables, we have:
V (x, ν, 0) = max [ex − K, 0]
so the Fourier transform of the payoff is:
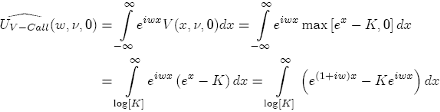
The Vanilla Call
We need to check when this integral actually converges and bear in mind that "w" can be any complex number. We need the exponential to decay as "x" becomes large, so that the integral converges. This ONLY happens if Im(w) > 1 and, when this is true, we can evaluate the integral with some simplification of which gives:
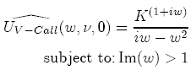
The Vanilla Put
Here conditions remain the same, except that this time the integral converges only if Im(w) < 0. When this is true, we get an identical transform:
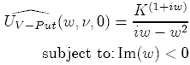
Digital Calls and Puts
For a digital call, the transformed payoff is:
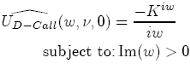
For a digital put, we have:
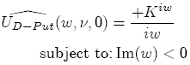
Prof. Klaus Schmitz
Next: The fundamental solution
Summary: Index