Let us consider the following SDE where the volatility σ and the drift µ are constants:
dS = Sµdt + SσdW (3)
Suppose that f (S) is a smooth function of S. If we vary S by a small amount dS, then clearly f also varies by a small amount. From the Taylor series expansion, we can write:
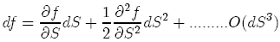
This result can be further generalized by considering a function of the random variable S and of time, f (S, t). We can expand f (S+dS, t+dt) in a Taylor series of (S, t) to get:
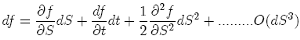 (4)
(4)
where the dots denote a remainder (O(dS3)) which is smaller than any of the terms we have retained. Now recall that dS is given by the SDE {3}. Here dS is simply a number, although random, and so squaring it, we find that:
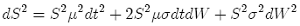 (5)
(5)
We now examine the order of magnitude of each of the terms in {5}
Since:
dW2 --> dt, as dt --> 0
the third term is the largest for small dt and dominates the other two terms. Therefore:
dS2 = S2σ2dt
If we substitute this result into {4} and retain only those terms which are relevant, we get:
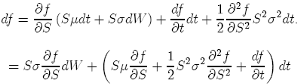 (6)
(6)
We can obtain the same result in an easy way by applying Ito’s lemma {1} directly to our SDE {3}.
Prof. Klaus Schmitz
Next: Applying Ito to the Hedging Portfolio
Summary: Index