Risk-Neutralization and No-Arbitrage

Now if we choose φ = ∂V/∂S, the square-bracketed terms from {7} disappear and change the Π to be deterministic, e.g. the portfolio is instantaneously risk-free (no random numbers are involved). Hence by the principle of no-arbitrage , Π must instantaneously earn the risk-free bank rate "r":

dΠ = rΠdt

Substituting the value of the portfolio:

dΠ = r (V − φS) dt

and combining this equation with {7}, dividing by dt and rearranging, we get:

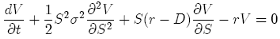(8)

This is the Black-Scholes equation and is a linear parabolic partial differential equation. In fact, almost all partial differential equations in finance are of a similar form. The Black-Scholes equation was first written down in 1969 but a few years passed, with Fisher Black and Myron Scholes justifying the model, before it was published. The derivation of the equation was finally published in 1973, although the call and put formulae had been published a year earlier.

Exact Solution for Black-Scholes Equation

We can say for the general Black-Scholes equation {8} that, for a European (vanilla) option that has boundary conditions or payoff:

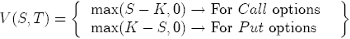(9)

we can find the explicit solution for V (S, T ):

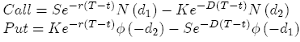(10)

where:

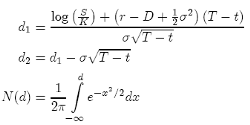
where N (d) is the standard normal cumulative distribution function (cdf ).

Prof. Klaus Schmitz

Next: Implied Volatility (Smiles and Skews)

Summary: Index