We can say that the General PDE for stochastic volatility {25} and the original Black-Scholes PDE {8} have a lot of similarity. If the boundary condition is the payoff of a standard European option (vanilla option):

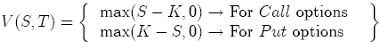
the exact solution for V (S, T ) in the Heston PDE {23} is:

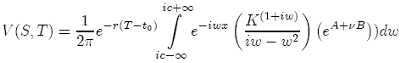(26)

x = log(S) + (r − D)(T − t₀)

τ = T − t₀

with the condition:

for Call options: Im(w) > 0

Put options: Im(w) < 0

and where:

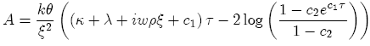
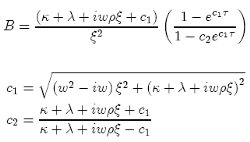
Important Remarks about Stochastic Volatility

The Black-Scholes exponential Brownian motion model provides an approximate description of the behavior of asset prices and a benchmark against which other models can be compared. The volatility parameter is a crucial component of the model. As observed in empirical studies, stochastic volatility aims to reflect the apparent randomness of the level of volatility. The prices of exotic options given by models based on Black-Scholes assumptions can be wildly inaccurate, because they are frequently even more sensitive to levels of volatility than standard calls.

Therefore, currently traders or dealers of these financial instruments are motivated to find models to price options which take the volatility smile and skew into account. To this extent, stochastic volatility models are partially successful because they can capture, and, potentially, explain the smiles, skews and other structures which have been observed in market prices for options. Indeed, they are widely used in the financial community as a refinement of the Black-Scholes model.

Prof. Klaus Schmitz

Next: Ornstein-Uhlenbeck Process

Summary: Index