The Heston model [6] (1993) is a special case of this scheme where γ = 1/2 and the market price of risk Λ. Furthermore, the real world drift is re-parametrized in the form:

ω − ζν = k(θ − ν)

Heston’s paper argues that there is evidence for the linear choice of Λ = λν. The partial differential equation (PDE) from the Heston model is then:

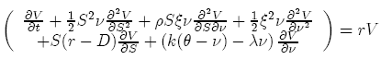(23)

The solution technique involves an "extended transform" which in this case is a conventional Fourier transform.

The SDEs for Simulation and the General PDE

The PDE from Heston model {SDE-23} follows the next SDEs (with correlation ρ between the noise terms):

dS = S(r − D)dt + S√νdW₁

dν = (k(θ − ν) − λν) dt + ξν^γ dW₂ (24)

However, if we try to be more general with respect to the second equation {24}, we need to represent it in the form:

dν = a(ν)dt + b(ν)dW₂

and applying Ito’s formulae {2}, we arrive to the General PDE for stochastic volatility:

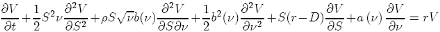(25)

This allows us to consider how to solve without reference to a particular volatility. In practice, we shall be driven back to the Heston class, but (see e.g. Lewis [11]) we can establish the solution for this more general case.

Prof. Klaus Schmitz

Next: Exact Solution for Heston Volatility

Summary: Index