Ito’s lemma is the most important result about the manipulation of random variables that we require. It is to functions of random variables what Taylor’s theorem is to functions of deterministic variables. It relates the small change in a function of a random variable to the small change in the random variable itself. The lemma is, of course, more general than this and can be applied to functions of any random variable. Suppose that X is described by a stochastic differential equation (SDE) of the form:

dX = A(X, t)dt + B(X, t)dW

where A(X, t) is called the drift term, B(X, t) the noise intensity term or volatility function and dW is a Wiener-Lévy process or Brownian motion.

• The one dimensional version

Thus given a smooth function f (X), Ito’s lemma says that:

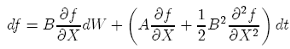
Thus given a smooth function f (X, t), Ito’s lemma says that:

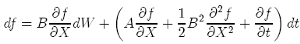(1)

• The two dimensional version

If X,Y satisfy the following SDEs:

dX = A(X, t)dt + B(X, t)dW₁

dY = C(Y, t)dt + D(Y, t)dW₂

where W₁,W₂ have a correlation "ρ" and thus given f (X, Y, t), Ito’s lemma says that:

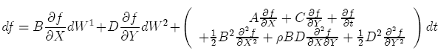(2)

Prof. Klaus Schmitz

Next: Taylor Series Expansion

Summary: Index