Clearly we wish to eliminate the stochastic component of risk by setting:

a = b = 0

so we rearrange the hedge parameters in the form:

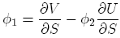
to eliminate the dS term in {20}, and

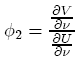
to eliminate the dν term in {20}.

The avoidance of the arbitrage, once these choices of φ₁, φ₂ are made, is the condition:

dΠ = rΠdt

dΠ = r (V − φ₁S − φ₂U ) dt (21)

where we have used the fact that the return on a risk-free portfolio must be equal to the risk-free bank rate r which we will assume to be deterministic for our purposes. Combining equations {20} and {21}, collecting all V terms on the left hand side and all U terms on the right hand side, we get:

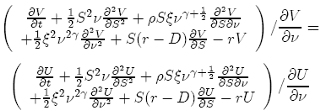
Now V , U are an arbitrary pair of derivative contracts. The only way that this can occur is when both sides of the equation are equal to some function depending only on S, ν, t. So we write both sides as f (S, ν, t), where f is the real world drift term less the market price of risk Λ.

f (S, ν, t) = ((ω − ζν) − Λ)

In doing so, we arrive to the General PDE for mean reversion stochastic volatility:

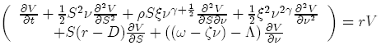(22)

Prof. Klaus Schmitz

Next: The Heston Model

Summary: Index