We begin by writing down the usual Geometric Brownian Motion SDE where the volatility σ is written as the square root of a variance ν:

dS = S(r − D)dt + S√νdW₁ (17)

and (r − D) is the deterministic instantaneous drift of stock price returns. The variance ν is constant in the original Black-Scholes model (1973). Now it is assumed to follow its own SDE in the form:

dν = ((ω − ζν) − Λ) dt + ξν^γ dW₂ (18)

where ξ is the volatility of volatility and ρ is the correlation between dW₁ and dW₂. This representation models mean-reversion in the volatility "σ" or variance "ν". Conventionally (ω − ζν) is called the real world drift. Λ(S, ν, t) is the market price of volatility risk, and it tells us how much of the expected return of V is explained by the risk (standard deviation) of ν in the Capital Asset Pricing Model framework.

Various economic arguments can be made (see reference [11] for example) that the market price of volatility risk Λ should be proportional to the variance ν. Then let Λ = λν for some constant or function λ. Furthermore, if the real world drift is re-parametrized in the form:

(ω − ζν) = &k(θ − ν)

we yield to:

dν = (k(θ − ν) − λν) dt + ξν^γ dW₂ (19)

where κ is the mean-reverting speed, θ is the long-run mean, λ is the market price of risk function, ξ is the volatility of volatility, and dW₁ (19) and dW₂ (19) are two Wiener processes (Brownian motion) with correlation coefficient, ρ. We use γ to generalize {19}. The six parameters κ, θ, λ, ξ, γ and ρ are assumed to be constant.

For our purpose, we will use the stochastic model {19} because it is both a general representation for all stochastic models that we outline in {13, 14, 15, 16}, and it uses the Heston parameters that are well known in the financial world.

Applying Ito to the Hedging Portfolio

We can not hold or "short" volatility as is, but we can hold a position in a second option to do hedging. So if we consider the valuation of the "volatility dependent instrument V ", we shall assume that we can take long or short positions in a second instrument U as well as in the underlying S. Now our candidate for an instantaneously risk-neutral portfolio Π is:

Π = V − φ₁S − φ₂U

The jump in the value of this portfolio in one time step is:

dΠ = dV − φ₁dS − φ₂dU − φ₁DSdt

where D is the dividend yield on the asset S. As is by now standard, the change in this portfolio in a time dt is given by:

dΠ = adS + bdν + cdt (20)

where:

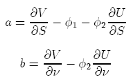
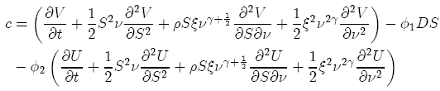
Prof. Klaus Schmitz

Next: Risk-Neutralization and No-Arbitrage

Summary: Index