Implied Volatility (Skews and Smiles): Most derivative markets exhibit persistent patterns of volatilities varying by strike. In some markets, those patterns form a smile curve. In others, such as equity index options markets, they form more of a skewed curve. This has motivated the name "volatility skew". In practice, either the term "volatility smile" or "volatility skew" (or simply skew) may be used to refer to the general phenomena of volatilities varying by strike.

Local Volatility (Dupire Equation): In 1994, Dupire showed that if the spot price follows a risk-neutral random walk and if no-arbitrage market prices for European vanilla options are available for all strikes K and expiries T, then the local volatility can be extracted analytically from these option prices. Stochastic Volatility (Heston Model): The aim with a stochastic volatility model is to incorporate the empirical observation that volatility appears not to be constant and indeed varies, at least in part, randomly. The idea is to make the volatility itself a stochastic process. In this document we present the exact solutions for a European option using both constant and Heston volatility.

Questions to be Considered: We can estimate the market view using the volatility which is implied by the market prices. Using this real information, we can simulate the future asset price path with its corresponding implied, local and stochastic volatility.

• How useful is it?

• Can we take advantage of this information to obtain a more accurate price for an exotic option and have a better understanding of hedging?

Using real market data obtained from newspapers, banks, television, the Internet (www.londonstockexchange.com), etc., such as the FTSE-100, Dow Jones, Nikkei or Dax, we can estimate the market view using the volatility "σ" which is implied by the market prices. Looking at the traded options section of the Financial Times of 4 February 1993 (table 1.1), we can get the options prices from the FT-SE INDEX.

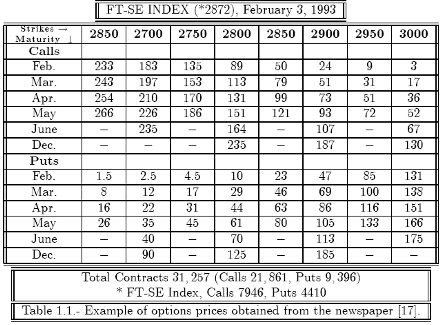
Using this real data, we can estimate (simulate) the future asset price path with its corresponding implied, local and stochastic volatility.

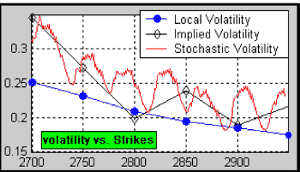
Figure 1.1.- Implied, local and stochastic volatility for real market data.

Prof. Klaus Schmitz

Next: Implied Volatility - Ito's Lemma

Summary: Index