Now we derive the Black-Scholes equation for a European option V with arbitrary payoff V (S, T) = Ψ(S). Let us construct a portfolio Π consisting of one option and a number "−φ" of an underlying asset. The value of the portfolio is:

Π = V − φS

where φ is constant and makes Π instantaneously risk-free. The jump in the value of this portfolio in one time step is:

dΠ = dV − φdS

Let us consider that the dividend yield is defined as the proportion of the asset price paid out per unit time, so then, at time dt, the underlying asset pays out a dividend D * S * dt. Since we receive D * S * dt for every asset held and since we hold "−φ" of the underlying, our portfolio changes to:

dΠ = dV − φdS − φDSdt

We suppose that the stock price S satisfies the following SDE:

dS = S(r − D)dt + SσdW

where "r" is the risk free bank rate, "D" is the dividend, and "σ” is the volatility for the stock price "S". Applying Ito’s lemma to V , we find:

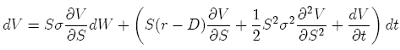
and so:

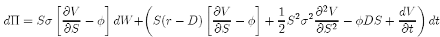(7)

Prof. Klaus Schmitz

Next: Risk-Neutralization and No-Arbitrage

Summary: Index