The phenomenon of the implied volatility smile shows that the Black-Scholes (1973) formulae tends to systematically misprice out-of-the-money and in-themoney options if the volatility implied from the at-the-money option is used. Stochastic volatility models are useful because they explain in a self-consistent way why it is that options with different strikes and expirations have different Black-Scholes implied volatilities (the volatility smile). More interestingly for us, the prices of exotic options given by models based on Black-Scholes assumptions can be wildly wrong.

The aim with a stochastic volatility model is to incorporate the empirical observation that volatility appears not to be constant and indeed varies, at least in part, randomly. The idea is to make the volatility itself a stochastic process. The candidate models have generally been motivated by intuition, convenience and a desire for tractability . In particular the following models have all appeared in the literature:

• Hull and White (ρ = 0, 1987 ) and Wiggins (ρ ≠ 0, 1987 )

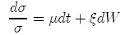(13)

• Scott (ρ ≠ 0, 1989)

d ln(σ²) = (w − ζ ln(σ²))dt + ξdW (14)

• Stein and Stein (ρ = 0, 1991)

dσ = (w − ζσ)dt + ξdW (15)

• Heston (ρ ≠ 0, 1993)

dσ² = (w − ζσ²)dt + ξσdW₂ (16)

The first model {13} was introduced by Hull and White (1987) who took (ρ = 0) and Wiggins (1987) who considered the general case (ρ ≠ 0). Here the volatility is an exponential Brownian motion, and it can grow indefinitely (or equivalently the logarithm of the volatility is a drifting Brownian motion). Scott (1989) considered the case {14} in which the logarithm of the volatility is

an Ornstein Uhlenbeck (OU ) process or a Gauss-Markov process. Themodels {13} and {14} have the advantage that the volatility is strictly positive all the time. The third model {15} was proposed by Scott (1987) and further investigated by Stein and Stein (1991). These authors specialized in the case (ρ = 0). In this model, the volatility process itself is an OU(Ornstein-Uhlenbeck) process with a mean reversion level "ω".

However, the disadvantage of this model is that the volatility σ could easily become negative. The final model {16} was proposed by Heston in 1993. The volatility is related to a square root process and can be interpreted as the radial distance from the origin of a multidimensional OU process. For small dt, this model keeps the volatility positive and is the most popular among them because of its two main features: it allows the correlation between asset returns and volatility, and it has a semi-analytical pricing formulae.

Even though continuous time models provide the natural framework for an analysis of option pricing, discrete time models are ideal for the statistical and descriptive analysis of the patterns of daily price changes. There are two main classes of discrete time models for stock prices with volatility. The first class, the autoregressive random variance (ARV) or stochastic variance models, is a discrete time approximation to the continuous time diffusion models that we outline in {13, 14, 15, 16}. The second class is the autoregressive conditional heteroskedastic (ARCH) models introduced by Engle (1982), and its descendents (GARCH, NARCH, etc.) can be defined in a variety of contents.

Generally speaking, we can say that they try to attempt to model persistence in volatility shocks by assuming an autoregressive structure for the conditional variances (time series). A large number of parameters are often needed to approximate the behavior of financial prices. Both the ARCH and ARV models give similar option prices (when the model parameters are appropriately matched). As shown in [1], these two models yield observational equivalents with respect to pricing options. We also notice that numerical procedures for computing option prices are faster for ARV, but estimation is simpler for ARCH. We concentrate our research on continuous time diffusion models and in the discrete time approximation of them (ARV).

There is a simple economic argument which justifies the mean reversion of volatility. Consider the distribution of the volatility of IBM in 100 years time as an example. If the volatility was not mean-reverting (if the distribution of volatility was not stable), the probability of the volatility of IBM being between 1% and 100% would be rather low. Since we believe that this is overwhelmingly likely that the volatility of IBM would, in fact, lie in that range, we can deduce that volatility must be mean-reverting.

Prof. Klaus Schmitz

Next: Coupled SDEs for Stochastic Volatility

Summary: Index