Given a set of N maps and probabilities (w, p), satisfying the properties i)- v) along with W_i : [0, 1] →[C_i, D _i) then the fixed points of M : M([0, 1]) → M([0, 1]) and T_p : F([0, 1]) → F([0, 1]), say ~µ and ~ F respectively, relate as follows

open full size image

Proof. From the contractivity of M and T_p, there exist

and

fixed points of M and T_p, respectively. Let

the thesis consists of proving

So we have:

open full size image

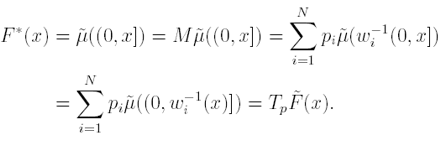
By the uniqueness of the fixed points, we get

The previous theorem allows to reuse the results of Forte and Vrscay (1995) and in particular gives another way of finding the solution of ( P ) in terms of ( Q ) at least on the simplex Π^N by letting δ_i = 0 in C^N. This is true in particular if we choose the maps as in T_F . To be more explicit: from now on the functional T_p is intended to have fixed maps w and all δ_i = 0.

Stefano M. Iacus, Davide La Torre

Next: 2.3 The choice of affine maps

Summary: Index