As we are mostly concerned with estimation, we briefly discuss the problem of choosing the maps. In Forte and Vrscay (1995) the following two sets of wavelet-type maps are proposed. Fixed and index

define

open full size image

and

open full size image

Then set

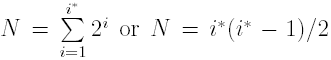
respectively. To choose the maps, consider the natural ordering of the maps ω_ij and operate as follows

open full size image

and

open full size image

respectively. Our quantile based maps are of the following type

where

and

are N + 1 equally spaced points on [0, 1]. For each given sets of maps w (W₁, W₁ and W_q) di erent p's will be solution of (Q) (or (P)). Whether the corresponding fixed point is closer to a given F in the three cases is not always clear. As an example, in Table 1 we show the relative performance of the approximation based on the quantity

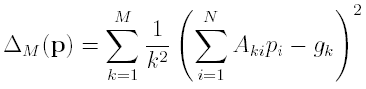
(that is an approximation of the collage distance), on the sup-norm d1 and on the average mean square error, AMSE. We also report the contractivity constant in both the space M([0, 1]) and the space F([0, 1]). Recall that the collage theorem for the moments establishes that, if g is the vector of moments of a the target measure µ (of a distribution function F) and is the moment vector of the invariant measure ¯µ_N of the IFS (w, p) then

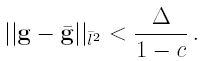
Table 1 shows that, at least in this classical example of the IFS literature, for a fixed number of maps N, T_N is a better approximator than M relatively to the sup-norm and the AMSE while the contrary is true in terms of the approximate collage distance Δ_M(p). As noted in Forte and Vrscay (1995), M uses not all the maps, in the sense that N0, the number of non null probabilities, is usually smaller than N'. It is evident that, two alternatives seem promising in the perspective of distribution function estimation: M with W₁ and T_N (i.e. M with maps W_q and pi = 1/N). Note that it is apparently simpler to use T_N because there is no need to calculate moments.

Stefano M. Iacus, Davide La Torre

Next: 3 Fourier analysis results

Summary: Index