The results presented in this section, taken from Forte and Vrscay (1998) Sec. 6, are rather straight forward to prove but it is essential to recall them since we will use these in density estimation later on.

Given a measure

the Fourier transform

where

is the complex
space, is defined by the relation

open full size image

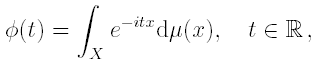
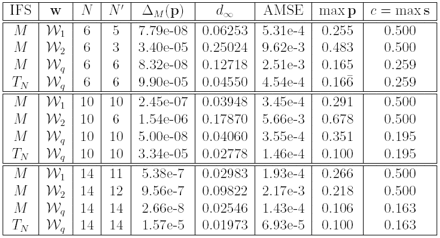
Table 1: Approximation results for the di erent N-maps IFS (w, p) for the targe distribution function F(x) = x²(3−2x) as in Forte and Vrscay (1995). N = number of maps used, AMSE = average MSE, max p is the contractivity constant of T_N in F([0, 1]), s is the contractivity constant of M in M([0, 1]). N' the number of non null probabilities. For the rest of the notation see text.

with the well known properties

We denote by FT(X) the set of all FT's associated to the measures in M(X). Given two elements

and

FT(X) the following metric can be defined

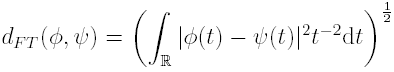
and the above integral is always finite (see cited paper). With this metric (FT(X), d_FT ) is a complete metric space. Given an N-maps affine IFS(w, p) and its Markov operator M it is possibile to define a new linear operator B : FT(X) → FT(X) as follows

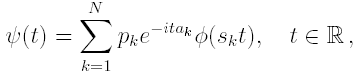
where

 is the FT of a measure µ and is the FT of ν = Mµ.

Stefano M. Iacus, Davide La Torre

Next: Theorem 8 (Forte and Vrscay, 1998)

Summary: Index