CHANGE LANGUAGE | Home > Technical Analysis Advanced > On fractal distribution function estimation and applications > 2.1 Minimization approach

On fractal distribution function estimation and applications

Introduction

Theoretical background for affine IFS

2.1 Minimization approach

Theorem 1

Theorem 2 (Collage theorem)

Theorem 3 (Forte and Vrscay, 1995)

2.2 Direct approach

Theorem 4 (Iacus and La Torre, 2001).

Theorem 5 (Iacus and La Torre, 2001)

Corollary 6

Theorem 7

2.3 The choice of affine maps

3 Fourier analysis results

Theorem 8 (Forte and Vrscay, 1998)

Theorem 9 (Collage Theorem for FT, (Forte and Vrscay, 1998))

4 Statistical applications

4.1 Asymptotic results for the quantile-based IFS estimator

Theorem 10

Theorem 11

Theorem 12 (Gill and Levit, 1995)

Theorem 13

4.2 Characteristic function and Fourier density estimation

5 Monte Carlo analysis

5.1 Applications to survival analysis

Final remarks

References

On fractal distribution function estimation and applications

2.1 Minimization approach

For affine IFS there exist a simple and useful relation between the moments of probability measures on M(X). Given an N-maps IFS(w, p) with associated Markov operator M, and given a measure

then, for any continuous function

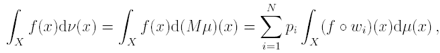
(2)

where

In our case

so we readly have a relation involving the
moments of

Let

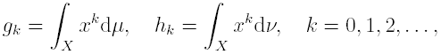
be the moments of the two measures, with g0 = h0 = 1. Then, by (2), with f(x) = xk, we have

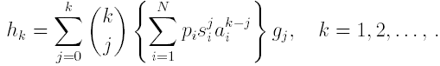
Recursive relations for the moments and more details on polynomial IFSs can be found in Forte and Vrscay (1995). The following theorem is due to Vrscay and can be found in Forte and Vrscay (1995) as well.

Stefano M. Iacus, Davide La Torre

PerformanceTrading.it ed il suo contenuto sono di esclusiva proprietà degli autori. E' vietata la riproduzione anche parziale di qualsiasi parte del sito senza autorizzazione, compresa la grafica e il layout. Prima della consultazione del sito leggere il disclaimer nella sezione [info].