Let F be continuous and

Then

has the Chung-Smirnov property.

Proof. In fact,

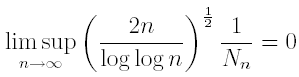
by hypotheses.

We can also establish the local asymptotic minimax optimality of our estimator when F is in a rich family (in the sense of Levit, 1978 and Millar 1979, see as well Gill and Levit, 1995, Section 6) of distribution functions. For any estimator F_n of the unknown distribution function F we define the integrated mean square error as follows

open full size image

where

is a fixed probability measure on [0,1] and E_F is the expectation under the true law F. What follows is the minimax theorem in the version given by Gil and Levit (1995).

Stefano M. Iacus, Davide La Torre

Next: Theorem 12 (Gill and Levit, 1995).

Summary: Index