Using the results of §3 is now feasible to propose a Fourier expansion estimator of the density function. We assume that all the minimal conditions to proceed in the Fourier analysis of this section are fulfilled. Thus, given and N-maps IFS(w, p), we have seen that the IFS estimator is the fixed point of the operator

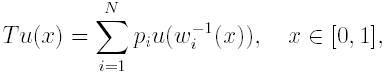
for any

or, equivalently, in the space of measure M([0, 1])

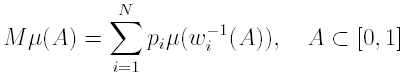
with maps and coefficients eventually estimated. Now, let

be the fixed point of the operator B in Section 3, i.e.

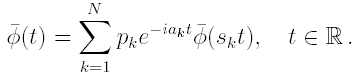
Then

is nothing else that an estimator of the characteristic function of f(·) where f(·) is the density function of the underlying unknown distribution function F(·) that generates the sample data X₁,X₂, . . . ,X_n. Now (see e.g. Tarter and Lock, 1993) it is possible to derive a Fourier expansion density estimator in this way.

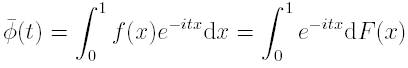
and, given

the density function f(·) can be rewritten as

open full size image

where

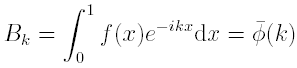
Denoting by

(the fixed point of) the characteristic function estimator based on quantiles

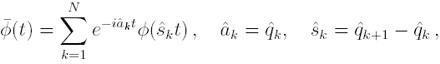
with

and

a density function estimator is the following

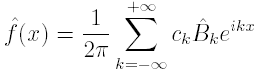(8)

where

is sequence of suitable multipliers not to be estimated and

One choice for the multipliers is c_k = 1 for

and c_k = 0 if

in such a case the estimator reduces to the raw Fourier expansion estimator

open full size image

A detailed discussion on which family of multipliers is to be choosen can be found in Tarter and Lock (1993) and can be applied to this case as well.

As it is well known, the fact that the Fourier expansion is a convergent series it is always possible to di erentiate or integrate it in order to obtain an estimator for the first derivative of the density

open full size image

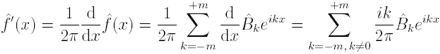
which is a particular case of (8) with c_k = ik

,k ≠ 0 and c_k = 0 and k = 0 or

We can also propose another distribution function estimator

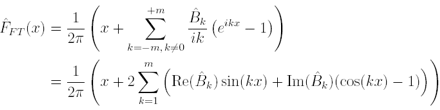(9)

open full size image

that can be used as a smooth estimator derived from IFS techinques instead of applying direclty the fractal

or

estimator. To conclude this section, we have to say that it is still possible to build IFSs in the space of density functions but direct application to estimation is less straightforward and this will be the object of another paper as it requires a di erent class of IFS systems, namely the local-IFS approach.

Stefano M. Iacus, Davide La Torre

Next: 5 Monte Carlo analysis

Summary: Index