Set X = [0, 1] and let µ and

with associated moments of any order gk and

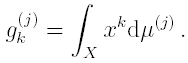
Then, the following statements are equivalent

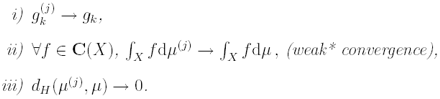
(here C(X) is the space of continuous functions on X). This theorem gives a way to find and appropriate set of maps and probabilities by solving the so called problem of moment matching.

With the solution in hands, given the convergence of the moments, we also have the convergence of the measures and then the stationary measure of M approximates with given precision (in a sense specified by the collage theorem below) the target measure µ (see Barnsley and Demko, 1985). Next theorem, called the collage theorem is a standard result of IFS theory and is a consequence of Banach theorem.

Stefano M. Iacus, Davide La Torre

Next: Theorem 2 (Collage theorem)

Summary: Index