Let X1,X2, . . . ,Xn be a sequence of i.i.d. random variables, each having a common continuous cumulative distribution function F of a real random variable X with values on [0, 1],
i.e.
![]()
We let F be such that
![]()
and
![]()
The empirical distribution function (e.d.f.)
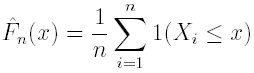
is one commonly used estimator of the unknown distribution function F. Here 1(·) is the indicator function. The e.d.f. has an impressive set of good statistical properties such as it is first order efficient in the minimax sense (see Dvoretsky et al. 1956, Kiefer and Wolfowitz 1959, Beran 1977, Levit 1978 and Millar 1979, Gill and Levit 1995). More or less recently, other second order efficient estimators have been proposed in the literature for special classes of distribution functions F. Golubev and Levit (1996a, b) and Efromovich(2001) are two of such examples.
It is rather curious that a step-wise function can be such a good estimator and, in fact, Efromovich (2001) shows that, for the class of analytic functions, for small sample sizes, the e.d.f. is not the best estimator. Here we study the properties of a new class of distribution function estimators based on iterated function systems (IFSs). IFSs have been introduced in Hutchinson (1981) and Barnsley and Demko (1985). These are particulary fractal objects, hence the title of this note. The fractal nature of IFSs based estimators implies that they are nowhere di erentiable and cannot be used to estimate density directly as in Efromovich
(2001) but, to this end, we will show a Fourier analysis approach to bypass the problem.
The paper is organized as follows. Section 2 is dedicated to the theoretical background of two constructive methods of approximating measures and distribution functions respectively, with support on compact sets. The first method essentially consists in the minimization< approach based on moment matching. This is rather common in the IFS literature. The second approach attacks directly the problem of approximating a distribution function with an IFS, by imposing conditions on the graph of the IFS. In practice, it is imposed to the IFS to pass through a fixed grid of points. IFS for measures are usually used not in a statistical context but mainly for image compression, here the main goal will be the problem of reconstructing a distribution function from sampled data. Even if we do not treat the problem here, the results are likely to hold for measures in any finite dimension [0, 1]k,
![]() .
.
In particular, the case k = 2 is interesting for image reconstruction. Section 3 recalls some results on the Fourier transform for affne IFS. These results are rather important for Section 4 where we propose two kinds of IFS estimators and a density estimator obtained as a Fourier series estimator. We also study the asymptotic properties of one of the two estimators. In particular, we will present a Glivenko-Cantelli theorem, a law of iterated logarithm property and the local asymptotic minimax effciency. Section 5 is dedicated to the Monte Carlo analysis on small sample sizes
Stefano M. Iacus, Davide La Torre
Next: Theoretical background for affine IFS
Summary: Index