Modello per la Media Condizionata

Quando si parla di rendimenti delle serie finanziarie, il primo interrogativo riguarda la ricostruzione del cosiddetto processo generatore dei dati: una rappresentazione matematica che leghi tra loro elementi diversi della sequenza di variabili casuali appartenenti ad uno o più processi. Il processo generatore dovrà, quindi, essere in grado di riprodurre le regolarità empiriche che si presentano all’interno della serie storica in termini di prezzi, rendimenti e volatilità.

L’ipotesi più semplice che si possa fare sui rendimenti finanziari è che siano generati da un processo cosiddetto “white noise”, dove le variabili casuali sono indipendenti e identicamente distribuite con media 0 e varianza costante. Se la distribuzione comune è quella normale si parla di “white noise gaussiano”. I rendimenti sono espressi come:

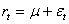
Dove μ è la media condizionate e εt è l’errore che viene spiegato come:

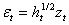
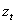       ~ iid(0,1)

Il processo WN è il metodo più semplice per descrivere i rendimenti finanziari che hanno valore atteso approssimativamente pari a zero.

Secondo Degiannakis e Floros(2010), per questo studio, la media condizionata deve essere modellata come un processo autoregressivo di primo ordine, ossia un AR(1), ed in parte è condiviso anche da Hsu e Wu (2009). Altri sostengono che la media debba essere trattata come una costante, quindi come un “white noise”, lo stesso pensano Donaldson e Kamstra (2004) e anche Becker, Clements, Coleman-Fenn (2009) che citano Cochrane: “i rendimenti si possono modellare in un orizzonte temporale molto lungo, come una costante”. Può essere interessante stimare la media dei rendimenti sia come un modello autoregressivo di primo ordine che considerando solo una costante (ossia un WN) e confrontare i risultati. Stimando la media come un WN si nota subito che il coefficiente non è accettato con una probabilità che rifiuta l’ipotesi nulla di significatività pari al 95%, mentre è diverso se la stimiamo come un AR(1) dove il coefficiente è accettato.

16: Coefficiente media come WN e AR(1)

Nell’analisi delle serie storiche, come in generale nell’analisi dei dati, possono essere specificati diversi modelli per rappresentare un dato campione di osservazioni e, in questi casi, si è chiamati a scegliere la migliore tra le possibilità alternative. Se esiste una specificazione generale che comprende, come casi particolari, gli altri modelli a confronto, la selezione può basarsi sulle verosimiglianze dei modelli stessi.

Dai valori ottenuti è possibile effettuare un confronto con il test di verosimiglianza: questo test consiste nell’uguagliare 2 modelli, uno vincolato e uno non vincolato, confrontando il valore dello loro log-verosimiglianze si trova un valore della statistica t, che poi va confrontato con il chi2 a seconda delle restrizioni che impongo. Se il valore di t è maggiore accetto il modello non vincolato, se è minore accetto quello vincolato. Nel confronto tra modelli, considerando il WN come vincolato e l’AR(1) come non vincolato, in modo da considerare una sola restrizione, dato che dal primo al secondo modello si considera una “innovazione” in più, e cioè il rendimento passato.

Figura 17: Test di verosimiglianza

Confrontando il valore della statistica t con il chi2 a 1 restrizione:

18,144>3,84

È evidente come il valore sia molto superiore al parametro di confronto, quindi si può rifiutare con certezza H0 (modello vincolato), accettando H1 (modello non vincolato), considerando migliore il modello con la media trattata come un processo autoregressivo. Per avere maggiori informazioni sulla bontà di adattamento di un modello, il criterio di informazione più noto e diffusamente utilizzato è quello di Akaike (AIC= Akaike info criterion), la cui espressione è:

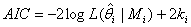
dove 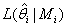 è il valore della funzione di verosimiglianza associata al modello  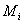quando i parametri sono 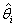, e 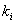 rappresenta la cardinalità di 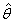, ossia il numero di parametri da stimare. La regola consente di confrontare i modelli, scegliendo quello in corrispondenza del quale si ottiene il valore minore di AIC (quindi il maggiore in valore assoluto). Confrontando i valori dell’AIC, il punteggio minore è dato dal modello che tratta la media come un AR(1), quindi si può sicuramente considerare migliore dell’altro.

Figura 18: AIC di WN e AR(1)

Alla luce di questi risultati si può affermare che, per i rendimenti dello S&P500 dal 2004 al 2010, modellare la media condizionata come un AR(1) dà una migliore stima del processo generatore dei dati. Tuttavia è un risultato inaspettato, dato che ci si poteva aspettare che si muovessero come un processo WN. Stima del modello auto regressivo di primo ordine:

Figura 19: Output di stima AR(1)

Osservando i coefficienti ottenuti nell’intervallo di valori considerato, il modello dice che i rendimenti di oggi sono calcolati come i rendimenti di ieri moltiplicati per un valore negativo: dato il coefficiente della stima del modello autoregressivo pari a            -0,066417 (P=0,0061), i rendimenti dello S&P500, per il periodo dal 2004 al 2010, sono dati dal valore passato moltiplicato per -6%.

Ma questo vale per l’intero intervallo considerato, è significativo verificare se la stima rimane uguale anche viene ristretto l’intervallo considerato. Per verificare questa ipotesi si possono ripetere le stime su intervalli più piccoli, in modo da testare la robustezza del modello.

Tenendo fisso l’estremo 2010 e diminuendo di 1 anno ogni intervallo si ottiene:

Figura 20: Stime della media autoregressiva ad intervalli decrescenti

Dalle stime si nota come il coefficiente sia sempre accettato nei diversi intervalli (tutte le probabilità sono p<0,05), il suo valore sia sempre negativo e più o meno uguale nel tempo, dal 2009 al 2010 la probabilità di non rifiuto è più alta, ma rimane comunque ad un livello accettabile.

Stime a 3 anni:

Figura 21: Stime della media autoregressiva su intervalli di 3 anni

Considerando un intervallo di 3 anni si ottengono buone stime, escludendo il periodo dal 2004 al 2007 dove la probabilità di non rifiuto è davvero molto alta, ma per il resto ottengo buone probabilità, coefficienti simili e negativi in tutti i periodi. Stime a 2 anni:

Figura 22: Stime della media autoregressiva su intervalli di 2 anni

Stime a 1 anno:

Figura 23: Stime della media autoregressiva su intervalli di 2 anni

Con le stime a 2 e 1 anno i coefficienti rimangono sempre significativi per proporzionalità e segno (escluso l’anno 2006 dove ho segno positivo), tuttavia le probabilità di non rifiuto sono più alte in alcuni periodi e accettate in altri, ciò evidenzia il fatto che questa specificazione per la media è migliore considerando intervalli temporali più lunghi. Tuttavia si possono ritenere delle stime accettabili e significative, per affermare che la media condizionata può essere modellata con un processo autoregressivo di primo ordine.

Per rafforzare questa analisi è interessante vedere la regressione lineare sui rendimenti della serie e i risultati che si ottengono, in termini di segno. Un anno finanziario è fatto più o meno da 250 osservazioni quindi, è interessante una regressione lineare su tutto il dataset a 3 anni (750 osservazioni), 2 anni (500 osservazioni) e 1 anno(250 osservazioni).

Cochrane, J.H. (2001), “ Asset Pricing”, Princeton University Press: Princeton, NJ. P.388

Mirko Cavallaro

Successivo: 3.4.1 Regressione Linere dei rendimenti su diversi intervalli Temporali

Sommario: Index