Under conditions i) to v):

1. T_p is an operator from

to itself.
2. Suppose that w_i(x) = x, P _i = p, and δ_i ≥ −p, then

3.

then T_p is a contraction on

with contractivity
constant c.

4. Let

such that T_pF₁ = F₁ and T_p* F₂ = F₂. Then

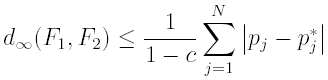
where c is the contractivity constant of T_p. The theorem above assures the IFS nature of the operator T_p that can be denoted, as in the previous section, as a N-maps IFS(w, p) with obvious notation. The goal is again the solution of the inverse problem in terms of p. Consider the following convex set:

open full size image

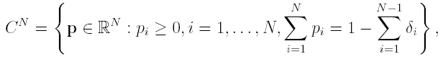
then we have the following results:

... in Theorem 5

Stefano M. Iacus, Davide La Torre

Next: Theorem 5 (Iacus and La Torre, 2001).

Summary: Index