We directly the fractal nature is to rescale the whole function in abscissa and ordinate and copying it a number of times obtaining a function that is again a distribution function. Consider
![]()
the space of distribution functions on [0, 1], then
![]()
is a complete metric space, where
![]()
Let
![]()
be fixed and let:
i)
![]()
![]()
![]()
with
![]()
and
![]()
ii)
![]()
are increasing and continuous;
iii)
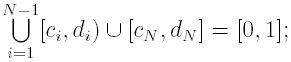
iv)
![]()
v)
![]()
On
![]()
we define an operator in the following way (see Iacus and La Torre, 2001):
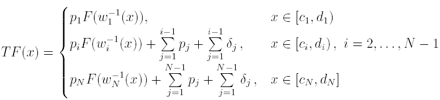 (4)
(4)
where
![]()
From now on we assume that wi are affine maps of the form wi(x) = six + ai, with 0 < si< 1 and
![]() .
.
Remark that the new distribution function TF is union of distorted copies of F; this is the fractal nature of the operator.
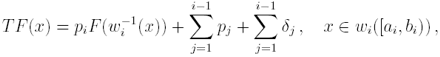 (5)
(5)
where
![]()
is fixed and:
i)
ii)
![]()
iii)
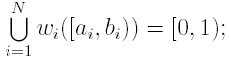
iv)
v)
![]()
We limit the treatise to affine maps wi as in Forte and Vrscay (1995), but the general case of increasing and continuous maps can be treated as well (see cited reference of the authors). From now on, we consider the sets of maps wi and parameters δi as given, thus the operator depends only on the probabilities pi and we denote it by Tp.
Stefano M. Iacus, Davide La Torre
Next: Theorem 4 (Iacus and La Torre, 2001).
Summary: Index