It is rather natural to propose two estimators for a distribution function, the Markov operator M^N with wavelets maps WL₁ and the T_N IFS. By Corollary 6 one can easily note that using the sample quantiles, it is not possible, in general, to achieve a precision ε = 1/N if the sample size n is less than N. But when n = N than, in the most defavorable case ε = 1/N, we just have the empirical distribution function for which we have the identity

for x = x_i, i = 1, . . . ,N + 1 and a linear interpolant between

and

Thus apparently, the worst thing one can do with the estimator T_F is to estimate the unknown distribution function with a linearized version of

The target of having ε = 1/100 means that at least 100 quantiles are needed and, non asymptotically, this is a to severe condition because, even having n = 100 observations, the empirical centiles are not good estimates of the true centiles. As we have seen in the previous section, Table 1, for having an error of order ε = 1/50 only 14 quantiles are needed around 1/3 of ε. So, as a rule of thumb we suggest to use a number of quantiles between n/2 and n/3. In oure monte carlo analysis we convain to use n/2. This strategy it is computationally heavy when n is large as the time to calculate the estimator increases too much, thus from a certain n it is better to use a fixed amount of quantiles. Our experience shows that N = 50 for large sample sizes is big enough, but for large sample sizes we suggest to use the empirical distribution function. Moreover, it has to be reminded that for N = 50 one can attend, in the worst case an error in sup-norm of 2%. Later on, we will give some theoretical results on the speed of convergence of T_P to F with respect to N.

The two estimators are the fixed points of the following IFS:
a) The Markov-Wavelets IFS

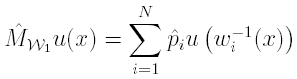
where

and the

are solutions of the quadratic problem (Q) with vector of empirical moments ^g instead of g. The number of empirical moments (m = N + 1) used is linked to the number of wavelet maps

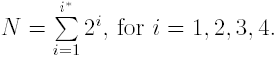
b) The quantile-based IFS

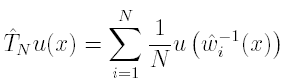
where

with q_i the empirical

and

In both cases

is any member of

Stefano M. Iacus, Davide La Torre

Next: 4.1 Asymptotic results for the quantile-based IFS estimator

Summary: Index