Let

be as in (6) with

as

If F is continuous, then

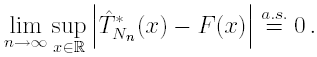
Proof. We can write

open full size image

and the first term can always be estimated by 1/N_n while the second one converges to 0 almost surely by Glivenko-Cantelli theorem. We can also establish a result of LIL-type. Recall that (Winter, 1979) an estimator F_n of F is said to have the Chung-Smirnov property if

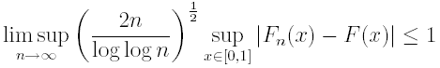
with probability 1.

Stefano M. Iacus, Davide La Torre

Next: Theorem 11

Summary: Index