Let (Y, d_Y ) be a complete metric space. Given an

suppose that there exists a contractive map f on Y with contractivity factor 0 ≤ c < 1 such that

If is the fixed point of

then

So if one wishes to approximate a function y with the fixed point of an unknown contractive map f, it is only needed to solve the inverse problem of finding f which minimizes the collage distance d_Y (y,f(y)). The main result in Forte and Vrscay that we will use to build one of the IFSs estimators is that the inverse problem can be reduced to minimize a suitable quadratic form in terms of the p_i given a set of affine maps w_i and the sequence of moments g_k of the target measure. Let

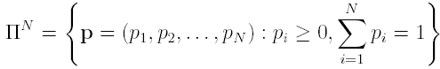
be the simplex of probabilities. Let w = (w₁,w₂, . . . ,w_n), N = 1, 2, . . . be subsets of W = {w₁,w₂, . . .} the infinite set of affine contractive maps on X = [0, 1] and let g the set of the moments of any order of

Denote by M the Markov operator of the N-maps IFS (w, p) and by

, with associated moment vector of any order h_N. The collage distance between the moment vector of

is a continuous function and attains an absolute minimum value Δ min on Π^N

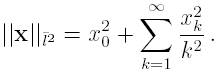
Stefano M. Iacus, Davide La Torre

Next: Theorem 3 (Forte and Vrscay, 1995).

Summary: Index