Asymptotic properties of the fixed points of both

and

derive as a natural consequence, by the properties of the empirical moments and quantiles. So, one can expect that, for a fixed number of N maps, the fixed point of

is a consistent estimator of the fixed point of M as the sample size increases and that the fixed point of

converges to the fixed point of T_N as well. But if we let N varying with the sample size n we can have much more, at least from

The fixed point

of the above operator,

satisfies

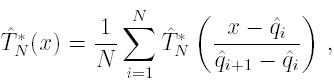
for real x. The following (Glivenko-Cantelli) theorem states that

has the same properties of an admissible perturbation of the e.d.f in the sense of Winter (see Winter 1973, 1979 and Yukish, 1989). Let us denote by N_n the number of maps and coefficients in the IFS so to put in evidence the dependency of the sample size n.

Stefano M. Iacus, Davide La Torre

Next: Theorem 10.

Summary: Index