As a corollary of the collage Theorem 4 we can anwser to the question: how many quantiles are needed to approximate a distribution function with a given precision, say ε ? The answer is: take the first integer N such that

This value of N is in fact the one that guarantees that the sup-norm distance between the true F and the fixed point

of T_F is less than ε. In general, this distance could be considerably smaller as shown in Table 1. Proof. To estimate d1(T_FF, F) we can slipt the interval [0,1] as

In each of the interval [q_i, q_i+1) the distance between T_F F ( x ) and F ( x ) is most 1/N. So, by the collage theorem, we have

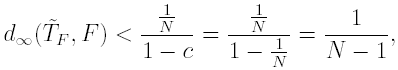
since

So, given ε > 0, it is suffcient to choose

To investigate the asymptotic behaviour of T_F it is worth to show the relation between this functional on the space of distribution function and the one proposed by Forte and Vrscay (1995) on the space of measures. Assuming that for any

we have

and

then T_F can be rewritten as

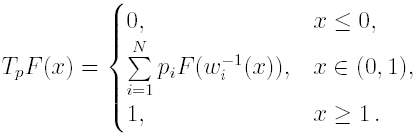
letting

Stefano M. Iacus, Davide La Torre

Next: Theorem 7.

Summary: Index