Ritornando alla questione di come il tempo possa essere discreto, come sostenuto da Mandelbrot e Fama, i quali hanno suggerito che la forma delle distribuzioni dei rendimenti potrebbe essere la stessa quando si modifica la scala temporale. Bene la proprietà dell'invarianza di scala sotto l'assunzione degli elementi indipendenti, venne trattata per primo dal matematico francese Paul Pierre Lévy47 e venne identificata con la nozione L-stabile. Nella teoria della probabilità una distribuzione alpha stabile di Lévy o distribuzione stabile è attualmente conosciuta come una famiglia di distribuzioni di probabilità caratterizzate da quattro variabili α ,B,μ e c ognuna delle quali assume un valore rilevante nella funzione Lévy.

Una distribuzione stabile ha la proprietà seguente: la somma di due variabili stocastiche che si distribuiscono secondo una certa forma funzionale (ossia secondo una certa distribuzione di probabilità) da come risultato una variabile che si distribuisce come le due sommate. In breve se x ed y si distribuiscono come una gaussiana allora anche z = x + y si distribuisce come una gaussiana. Questa è una proprietà di invarianza nel senso che due grandezze che seguono una stessa legge matematica, se sommate, continuano a seguire la stessa legge.

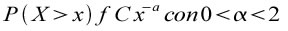
Per essere più precisi se una variabile X1 e X2 sono distribuite in accordo alla distribuzione stabile

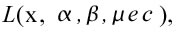
e se

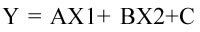
è una combinazione lineare delle due, allora esiste un valore di D ed E tale che DY+ E è distribuito come una distribuzione stabile

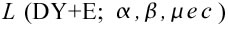
o, ugualmente, Y è distribuito come una distribuzione stabile

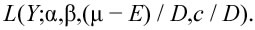
Se E = 0 per tutte le A, B, C, allora Y si dice che ha una distribuzione rigorosamente stabile. Le distribuzioni stabili risultano importanti anche per la spiegazione del Teorema del Limite Centrale e della teoria dell'auto-similarità delle serie storiche del cotone, dalla quale Mandelbrot partì per studiare la multi-frattalità dei dati finanziari della materia prima oggetto di studi.

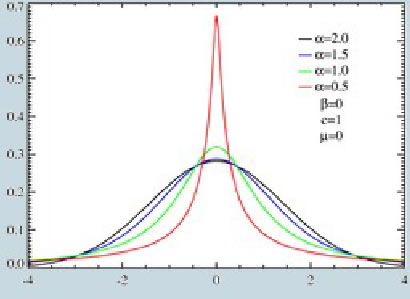
Illustrazione 22: Esempi di funzioni di distribuzione Lèvy

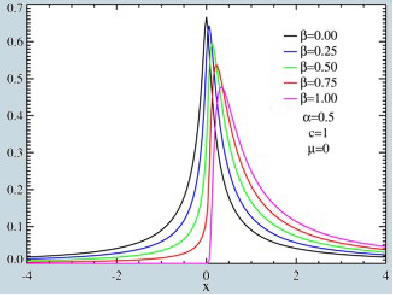
Illustrazione 23: Esempio di funzioni di distribuzioni Lèvy con valori di skewness diversi Lèvy

Come sottolineato in precedenza, i parametri che rientrano nella formula di Lévy, assumono valori diversi in funzione della distribuzione della probabilità, in effetti avremo per un valore di α pari a due avremo una curva di distribuzione normale, visto che il parametro alfa varia tra [0,2], per la distribuzione di Cauchy α è pari ad 1 mentre per la distribuzione di Lévy α è pari 1/2

Il coefficiente B è definito parametro di skewness che varia a seconda della tipologia delle distribuzione della probabilità, ad esempio per la distribuzione normale e Cauchy il valore del B è pari a zero mentre per la distribuzione di Lévy è B = 1 Il valore di B invece risulta una media della misura centrale, potendo assumer valori reali diversi dal parametro α In conclusione il parametro c, viene definito parametro di scala o parametro della dispersione e nella distribuzione normale assume un valore uguale alla sua deviazione standard, quindi un valore finito, mentre nelle distribuzioni stabili non normali il coefficiente c assume valori infiniti. Le variabili casuali citate, sono utili per generare moti casuali nel tempo continuo.

---

[46] Nell'Appendice al capitolo 3 saranno esposte alcune dimostrazioni de L-Stable Model.

[47] P.P.Lévy (Parigi 15 Settembre 1886, Parigi 15 Dicembre 1971) è stato un importante matematico e statistico francese del XX Secolo che ha focalizzato i suoi studi principalmente sulla teoria della probabilità. Ha studiato all'Ecole Polytechnique di Parigi dove a soli 19 anni pubblicò il suo primo lavoro. Successivamente si dedicò allo studio delle equazioni differenziali ed alle derivate parziali.

Successivo: 3.1.2 Fractional Brownian motion e Long dependance

Sommario: Indice