To my mind, the influence of sentiment on asset prices is best seen through options. However, traditional option pricing formulas involve interest rates. For this reason, I analyze the impact of sentiment on the term structure of interest rates in this section, and move to options thereafter. Theorem 3 below describes the relationship between the term structure and the representative trader’s parameters.

Theorem 3

Let 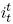denote the gross return to a risk-free investment in which one real dollar is invested at date 0 and pays off t periods later. The discount factors which are based upon (5) and define the term structure of interest rates have the form:

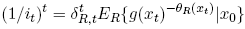(16)

where E_R is the expectation under the representative trader’s probability distribution. Equation (16) follows directly from (7) and the fact that the term structure is based on securities that offer a fixed payoff across all date t−states. This equation makes explicit the connection between the yield curve and the beliefs of the representative trader.22 The equation captures how interest rates evolve in terms of the discount factor θ_r,t the parameter θ_r, and the expectations of the representative trader E_R. Economists have long been puzzled by the fact that the expectations hypothesis of the yield curve fails to hold.

See Campbell (1995).23 In the remainder of this section, I briefly discuss the effect of sentiment on the term structure of interest rates, and the expectations hypothesis. As Ingersoll (1987) points out, there are several definitions for the expectations hypothesis of the term structure. I discuss two versions. The first is the pure version in which the forward rate equals the expected future spot rate. The second version states that subject to a time-invariant risk premium, the expected return to holding short term default-free securities is the same as the return to holding long term default-free securities. This version appears in the empirical work of Backus, Foresi, Mozumdar, and Wu (1997), and Roberds and Whiteman (1997).

The representative trader holds the market portfolio and consumes its dividends. Notably, a representative trader for whom C _r(x₀) = 1, consumes the cumulative dividend growth rate g _t = g(x_t). The expectations hypothesis is driven by the fact that at the margin, the representative trader is indifferent to substituting default-free bonds with long term maturities with those of default-free bonds with shorter maturities in his portfolio. For example, if we consider t = 2 as the long term and t = 1 as the short term, then indifference at the margin implies that:

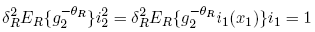
That is, the marginal utility of a dollar invested in either the short-term bond or the longterm bond is equal to the marginal utility of a dollar, which is unity. For ease of notation the x₂ argument in θ_r is suppressed, as is the x₀ associated with the conditional expectation in (17). Define the date 2 forward rate by:

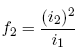
I note that (17) can be rewritten to obtain a condition that relates the spot and forward interest rates, a relationship often used to test the expectations hypothesis. When equation (19) below holds, the representative trader is indifferent to substituting a long bond for a short bond in his portfolio.24 This condition is derived using (1), (16), and the fact that the representative trader consumes the cumulative growth rate of the market portfolio. We have:

Theorem 4

Equation (19) implies that there are three impediments to the validity of the expectations hypothesis. The first is a nonzero risk premium that interferes with the pure expectations hypothesis, which states that the forward rate equal the expected spot rate. In general, the right-hand-side of (19) is nonzero.

As for the version of the expectations hypothesis that requires a nonzero risk premium but requires it to be time invariant, there are two additional impediments. First, the expectations hypothesis requires that the expectation in equation (19) be taken with respect to the objective distribution II. However, in (19), the expected spot rate is computed relative to the representative trader’s beliefs PR, not the objective process II. The point is that when Λ ≠ 0, the representative trader holds erroneous beliefs.

The final impediment concerns the stability of the risk premium, given the covariance term in (19). Let Z ₂ be the long bond. Since the risk premium is given by well known expression

the expectations hypothesis requires that the preceding covariance vary inversely with the spot rate i1. But by its nature, heterogeneity induces time variation into this covariance: recall the discussion about time variation in both θ_r and δ_r.25

Prof. Hersh Shefrin

Next: Risk-neutral Densities and Option Pricing

Summary: Index