How sensitive is the objective return distribution of the market portfolio to sentiment? The answer to this question depends on the representative trader’s risk tolerance, as the following theorem demonstrates.

Theorem 8 The x0-price q! of the market portfolio has the form:

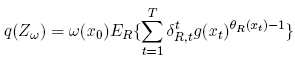(27)

Let r_ω(x₁) denote the return to holding the market portfolio from x₀ to the beginning of x₁. Then:

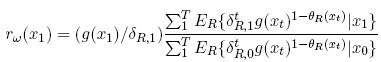(28)

In (28) the base from which growth is measured in the numerator is ω(x₁), whereas in the denominator the base is ω(x₀). The probabilities that underlie the return distribution for the market portfolio are given by Π. The support of the distribution is given by (28). Theorem 8 establishes how beliefs affect the support. The return to the market portfolio is a product of three terms, the growth rate in aggregate consumption, the inverse of δ_R, and the ratio of two expectations. To interpret expression (28), consider the case of logarithmic utility, meaning the case when θ_R = 1. Here, the expectation ratio in (28) is unity, so the return to the market portfolio is g(x₁)/δ_R. This implies that the return on the market portfolio is the consumption growth rate, scaled by the inverse discount factor. Scaling is necessary with discounting in order to induce saving. Take the logarithmic situation as the base case, and consider how r_ω changes relative to the base case as we increase the value of θ_R.

When δ_R > 1, the expectation ratio in (28) is not unity. Notice that the numerator of the expectations ratio is conditional on the x₁ while the denominator is the same expectation conditional on x₀. Because of the different bases from which growth is measured in numerator and denominator, a positive trend in expected growth rates leads the expectation ratio in (28) to lie above unity. Hence theorem 8 implies that a shift in optimism about consumption growth causes the return r_ω to be higher than its value under logarithmic utility. In other words, theorem 8 demonstrates how the value of θ_R affects the sensitivity of the return distribution of the market portfolio to trader beliefs.

Under logarithmic utility, the support of the return distribution is independent of traders’ beliefs. Theorem 8 makes clear that the logarithmic utility case is special. The lower the representative trader’s risk tolerance, the greater the influence of expectations on the value of r_ω. Notice that I used this property in the development of the second and third option pricing examples in section 8.

There is an additional point to notice about the impact of lower risk tolerance. It strengthens the correlation between the return on the market portfolio and the change in the yield curve. This can be seen by comparing (16) and (28).

Prof. Hersh Shefrin

Next: Contrasting Heterogeneity in Beliefs With Heterogeneity in Risk Tolerance

Summary: Index