Consider a financial market with H individual traders. Time is discrete, with a set of dates indexed t = 0, 1, 2, ... , T. At the beginning of each date, new information s is revealed. Call s a state, and assume that it belongs to a finite set S = {si}. Let st ε S denote the state revealed at date t. The public information at the beginning of t is denoted by the trajectory xt = (s0, s1, ... , st). That is, uncertainty unfolds according to a tree whose nodes are the date event pairs {xT}. Let II(xT) denote the objective probability attached to the occurrence of xT . I assume that the probability attached to a trajectory xt is derived from the terminal node density {II(xT)} as follows:
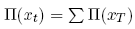
where a terminal node xT is in the summation if and only if xt is an ancestor node of xT . In this section, I assume that all information is held in common, and trading is costless. At the outset of date 0, trader h holds an initial portfolio ωh. If h holds ωh through date t, and date-event pair xt materializes, then h receives dividend ωh(xt) during
date t. The symbol ω = ∑ωh denotes the unlevered market portfolio.12 In equilibrium, the consumption growth rate
.
A financial security is represented as a vector Z = [Z(xt)] where Z(xt) is the amount which one unit of the security pays its owner at xt. Assume that the following securities are available for trade at every date t:
(1) Zero coupon, risk-free bonds: these bonds underlie the term structure of interest rates. Assume that a zero coupon bond maturing at any date t is available for trade at any date before t.
(2) The market portfolio: this security is denoted by Zω, and is a scalar multiple of ω.
(3) European put and call options on the market portfolio. I assume that we can guarantee markets to be complete by allowing enough variation in the option exercise prices. A call option issued at xt has an exercise price of K, expires at date t + j, and pays max{qω(xt+j) − K, 0}, where qω(xt+j) denotes the price of the market portfolio on the xt+j-market. A put option is analogous to a call option, but returns max{0,K − qω(xt+j)}.
Since markets are assumed to be complete, there are state prices that underlie security prices. Let v(xt) denote the price of an xt-state contingent claim, and v = [v(xt)]. I take x0 as numeraire: that is, v(x0) = 1. On the date 0 market, the price qz(x0) of security Z = [Z(xt)] is v • Z. On the xt market, the price qz(xt) of Z is the v-value of the Z-payoffs from date t on, divided by v(xt).[13]
A trader’s wealth at the beginning of t consists of the market value of his xt−1
portfolio, including dividends paid in xt. The trader then divides his xt-wealth into a portion to be consumed at t, and a portion to be saved. The saved portion is invested in the securities which comprise his xt-portfolio. Denote trader h’s net trade of the xt contingent commodity by zh(xt). Then the consumption vector ch = [ch(xt)] is given by
Ch = ω h + Z h.
The beliefs of trader h are represented by a subjective stochastic process P h on the trajectories. Hence, P h(xt) is nonnegative, and sums to unity for each t. Moreover, for each t, P h(xt) is determined by conditioning on the probabilities P h(xT ) that attach to the
terminal date T. I assume that each trader has a utility function featuring constant relative risk aversion. That is:
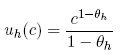
where
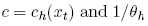
is h’s risk tolerance parameter. Furthermore, h’s preferences are additively separable over time and trajectories. Hence preferences are representable as the sum of weighted utilities, with weights Dh(xt), where Dh(xt) takes the form of a discounted probability
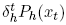
. Here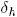 
is a discount factor satisfying 0 < 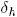< 1.
Every trader is assumed to choose his consumption plan ch by maximizing the sum of weighted utilities
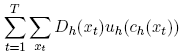(2)
subject to the lifetime budget constraint
.
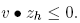Denote trader h’s x0-wealth by
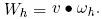
Then h’s demand function is:
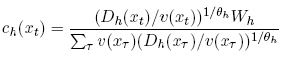(3)
Note that in (3) the pattern of the consumption profile is keyed from wealth W h, in that (3) specifies the fraction of wealth W h which is to be consumed in each date-event pair x t. In the discussion below, it will be useful to consider the consumption profile as being keyed to initial consumption C h(x0) rather than to Wh. Note that v(x0) = 1 since x0 is taken as numeraire. Hence the denominator of (3) is equal to W h/ch(x0), so that by substitution, h’s consumption growth rate is given by:
(4)
Prof. Hersh Shefrin
Next: A Representative Trader Characterization
Summary: Index