In this section I present three equivalent option pricing expressions. The first expression is developed in theorem 5. This expression is based on the standard risk-neutral density approach, and involves the arguments used to demonstrate how discrete time option pricing formulas converge to the Black-Scholes formula in the limit. See Cox, Ross, and Rubinstein (1979), and Madan, Milne and Shefrin (1989). In the next section, I extend the argument to establish why sentiment prevents the conditions that underlie Black-Scholes from holding. In theorem 6, I present a second option pricing expression that demonstrates how traders’ beliefs, operating through the beliefs of the representative trader, affect option prices. The risk-neutral based option pricing expression in theorem 5 obscures the relationship between traders’ beliefs and the prices of options. And the traditional risk-neutral approach to option pricing appears to have led researchers to the view that option prices are independent of traders’ beliefs, since that is the case in partial equilibrium option models.

However, as I demonstrate in section 8, traders’ beliefs impact option prices. The third option pricing expression reflects what I call a “snapshot in time” approach. The “snapshot in time” expression, also described in theorem 6, depends only on variables associated with the expiration date. In particular it relies on the long-term interest rate and the risk-neutral density at the expiration date. This contrasts with the first expression, in theorem 5, that relies on the co-evolution of the short-term interest rate process and the risk-neutral process over the life of the option.

The “snapshot in time” approach is useful for pointing out that the differences between continuous time option pricing models and discrete time option pricing models are less important than the character of the risk-neutral process. This approach serves to provide a link between the two modeling techniques. Theorem 5 below describes the first option pricing formula, expressed in terms of the risk-neutral process and the process for short-term interest rates.

Theorem 5 Given (7), the general expression for the price of a European call option on a security Z, featuring exercise price K and expiration date t, is determined as follows. (1) Let S(x_t−1) be the set of successor nodes x_t to x_t−1. The risk-neutral density η(x_t) associated with event {x_t}, conditional on x_t−1, is defined by:

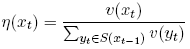
Let AE denote the event

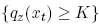
in which the call option is exercised, and P_η{A_E} be its probability under the risk-neutral density P_η. The product of the single period interest rates defines the cumulative return it

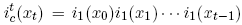
to holding the shortterm risk-free security, with reinvestment, from date 0 to date t. Then the x₀-price of the call option is given by:

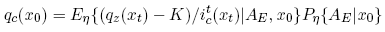(21)

Risk-neutral density pricing equations, such as (21) tend to obscure how the properties of the representative trader’s beliefs affect asset prices. As I mentioned above, I present two alternative option pricing expressions.

Theorem 6 (1) Given (7), the price of a European call option on a security Z, featuring exercise price K and expiration date t, is determined as follows. Let A_E denote the event

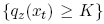
, in which the call option is exercised, and P_r{A_E} be its probability under the representative trader’s probability distribution P_r. Then qc satisfies:

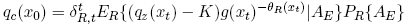(22)

(2) Define the t-step probability distribution Φ(x_t) over date t events x_t, conditional on x₀ as follows:

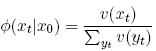(23)

Then q _c satisfies:

Expressions (22) and (24) describe the direct impact of the representative trader’s beliefs on call option prices. (22) prices the option using the state price representation (7)[26] (24) indicates the connection between the term structure and option prices, in that the t−period bond is used to price the option.

Prof. Hersh Shefrin

Next: Option Pricing Examples

Summary: Index