In this section, we consider overconfident traders with market power in a
pairwise contest. Consider a large economy with N risky assets, whose values˜v1, ˜v2.....˜vN are independently and identically distributed at the end of each period. For simplicity, normalize the risk-free rate r to zero. The economy is populated with risk-neutral informed traders of two possible types: rational and nonrational. At the beginning of each period, informed traders do not know which type of the other informed traders they are going to face, since they have the possibility of trading against rational and nonrational traders.

Then, nature draws randomly a pair of informed traders from the current distribution of the population for each market n (n = 1, 2, ...... N), independently across all N markets. Thus, in each market there are four possible type combinations of the two informed traders thus drawn. Denote the possible type combinations by

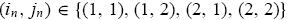
, where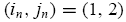

means that the first informed trader drawn in market n is a type-1 (rational) trader and the second informed trader is a type-2 (nonrational) trader, etc. The probability of each type-combination drawn in each market is governed by the current population state x(t) D (x1(t), x2(t)) in the large economy. Specifically, with probability the

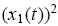pair of informed traders thus drawn is both rational, with probability

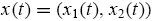
the pair of informed traders consists of one rational and one nonrational, etc. In each period, after a particular type combination

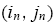is thus drawn in market n, it becomes common knowledge to all market participants. These two informed traders then participate in one-shot trading along with liquidity traders and market makers in the market, based on the trading mechanism of Kyle and Wang (1997)2 . For simplicity, we suppress the time index t in what follows, but
it should be understood that all random variables discussed below depend on it. Informed trader j ( j D 1; 2) drawn in market n has a unique access to a private signal

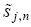
about the asset’s value 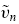in the market. The correct distribution of the
signal is

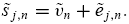
The forecast errors 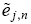’s are independently and identically
distributed for j = 1, 2 and n = 1, 2........ N. However, the informed trader’s belief about his or her signal depends on his or her type. In particular, informed trader j thinks his signal is

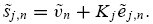
If the trader is rational, his or her belief reflects the correct distribution, i.e.,

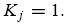
On the other hand, if the trader is not rational, then his or her subjective belief is parameterized by K _j = K, where K is a nonnegative misperception parameter such that

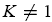
. Furthermore, a nonrational trader is overconfident if his or her subjective distribution is too tight, i.e.,

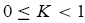
or underconfident if it is too loose, i.e., K > 1 (Oskamp (1965), Alpert and Raiffa (1959), Einhorn and Hogarth (1978)). With risk-neutrality, informed trader j submits a market order

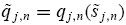
to maximize his or her conditional expected trading profit,

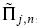
, given his private signal

i,e.

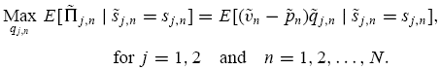
The subscript j of the expectation operator denotes that the expectation is based on trader j’s belief. Liquidity traders in market n submit a random quantity 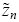and their trading across markets 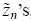are independently and identically distributed. Competitive market makers (also called trader 0) observe the order imbalance

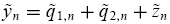
and then clear the market by setting the asset price 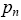equal to the conditional expectation of the asset value 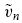given the observed order imbalance as 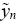follows:

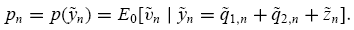
The subscript 0 of the expectation operator denotes that the expectation is based on rational beliefs. Exogenous variables

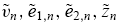are independently and normally distributed with means zero and variances

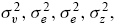
, respectively. The quality of the private signals may be measured (inversely) by the noise-to-signal ratio

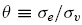
The amount of noise trading in each market may be measured by a
normalized ratio

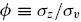
. Kyle andWang (1997) show that the one-shot model,
given the type combination 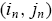, has a unique linear equilibrium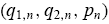
as follows,

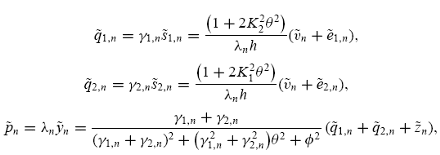
where h is a strictly positive constant, given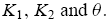
The intensity parameters 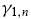and 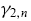and liquidity parameter ¸n depend on the noise-to-signal ratio 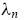, the noise trading ratio 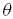, the misperception parameter K, and the type combination 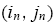drawn at the beginning of the period. Moreover, for the same type combination

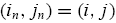the three parameters are uniquely determined, regardless of what n is. Hence, without loss of generality, we may
suppress the market index n and write

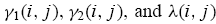as the three parameters identical in those markets with the same type combination (i, j). With
the above equilibrium, the type-i trader’s return, given a type-j opponent in market n, denoted by

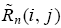,is obtained as follows:

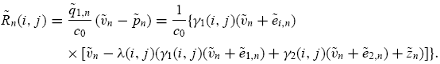
Note that in the last equality of (15)wesubstitute for

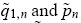from Eq. (12)–(14). The individual type-i trader’s return in market n,

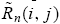, is stochastic because the realization of the type combination (i, j) in each market has a probability

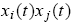. Hence, we may identify the subsequence of those markets with the same realized type combination (i; j) as

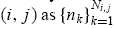. In each market n_k , the individual type-i trader’s return,

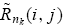, is still stochastic because it depends on the exogenous random variables:

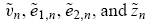Note, however, that these exogenous variables
are all independently and identically distributed across markets. As a result, the individual type-i trader’s returns in these markets,

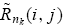, are independently and identically distributed too. The average return of the type-i traders facing type-j opponents
across these markets is given by

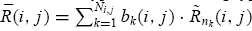, where the weight

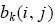is the relative size of the type combination (i, j ) in market n_k
such that the weights across these markets sum to one, i.e.,

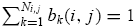. If the population share of each group in the economy is bounded below from zero, then the number of markets of each type combination (i, j ) becomes sufficiently large in a large economy, i.e.,

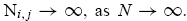Moreover, in the large economy the average return of the type-i traders across these markets converges
to the expected return of a representative type-i trader in these markets, denoted by

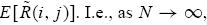
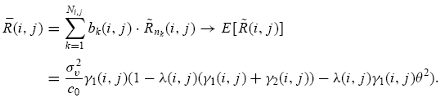
Note that the last equality in (16) is obtained by taking expectations on both sides of Eq. (15). For simplicity, we omit the subscript 0 for the expectation operator, but it should be understood that the expectation is based on the correct distributions, i.e., rational beliefs. In addition, we drop the market index n_k when we write the expected return,

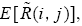, because the individual returns

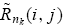for all n_k are independently and identically distributed across these markets. Equation (16) highlights the strategic nature of the pairwise contest between the two randomly matched informed traders since each trader’s expected return depends also on the other trader’s type. The average return of the type-i traders across all markets in the economy,

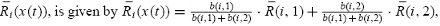
where the weight b(i, j ) is the relative size of the type combination (i , j ) in the economy such that the weights sum to one, i.e.,

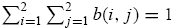In the large economy, the relative size of each type-combination approaches the corresponding population distribution, i.e.,

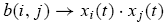As a result, the average return of the type-i traders converges to the expected return of the representative type-i
trader,

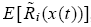in the large economy. I.e., as ,

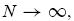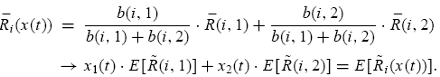
Applying the payoff function, i.e., the expected return, in (17) to the general population dynamic in (9) yields the specific population dynamic for type-2 traders in the pairwise contest as follows:

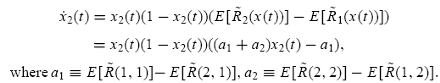
The population dynamic in (18) depends crucially on the two return parameters, a1 and a2, where a1 represents the expected return differential between a type-1 trader and a type-2 trader, both having a type-1 opponent; a2 represents the expected return differential between a type-2 trader and a type-1 trader, both having a type-2 opponent.We may partition the population dynamic (18) into four mutually exclusive categories, depending on the two return parameters: (I) a1 > 0; a2 < 0; (II) a1 < 0; a2 > 0; (III) a1 > 0; a2 > 0; and (IV) a1 < 0; a2 < 0. Following the standard analysis of the dynamic equilibrium in the corresponding evolutionary game, we obtain the asymptotically stable equilibria for each category. The results are shown in Theorem 1 in the next page

Prof. F. Albert Wang

Next: Theorem 1

Summary: Index