Let A = { a1, …, an} be the set of entities or, in equivalent terms, the collective of units that are to be ranked, and let cm: A2 :-->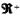 be the preference function between two entities defined following the multiplicative scheme. In this case:

cm(ai, aj) = rij; i,j=1, …, n, (1)

measures how many times alternative ai is preferred to alternative aj. In this case:

(2.1) (2.2) (2.3)

Coherence between the bilateral comparisons requires satisfaction, besides the identity property:

rii = 1 ; i=1, …,n , (3)

also of the reversibility property:

rij = 1/rji ; i, j=1, …, n , (4)

while the coherence between multiple comparison requires also the transitive propriety:

rij = rikrkj ; i, j = 1, …, n . (5)

As is well known, in this case it is possible to rank the entities ai by assigning to each of them a value wi determined up to a multiplicative constant which depends on the choice of the unit of measurement, so that:

rij = wi/wj; i, j = 1, …, n. (6)

If instead the additive scheme is followed, the assessment of the preferences between two entities is expressed by a function ca: A2 : --> ,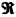

ca(ai,aj) = sij; i, j = 1, …, n . (7)

which measures to what extent alternative ai is preferable aj. In this context:

(8.1) (8.2) (8.3)

The properties of identity and reversibility and the transitive property are respectively expressed by the relations:

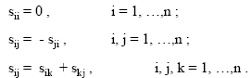(9) (10) (11)

In this context too, if the preference function (7) satisfies the transitive property (11), it is possible to rank the entities ai by associating with each of them a value vi determined up to an additive constant, so that:

sij = vi – vj ; i, j = 1, …,n . (12)

The formal connection between the multiplicative and additive schemes is easily stated: suffice it to consider the logarithmic transform of relations (1)–(6) to link them to the corresponding relations of the additive scheme. Vice versa, performing an exponential transform of the latter brings us back to the relations of the multiplicative scheme. However, a distinction should be drawn between the formal analogies and the substantial aspects that induce a preference for one scheme rather than the other according to the problem to be addressed.

Once this choice has been made, however, one must proceed with logical coherence in defining the indicators measured on the individual units. Particular account should be taken of the linkages between the functional specification of the indicators, according to whether they are associated positively or negatively with desirability, and the synthesis functions used to perform the comparisons and rank the units.

This, I believe, is an aspect of fundamental importance which is too often neglected. For particularly wide-ranging and significant treatment of it, as regards theory and practical application, see Vitali and Merlini (2001), and for certain essential specifications developments the recent study by Merlini (2001). In what follows I shall examine the PROMETHEE[2], one of the best known and most widely used methods of multicriteria analysis,[3] to show that it can been related to the coherent additive scheme.

I shall also show that the passage from PROMETHEE I to PROMETHEE II, proposed as an empirical procedure with which to construct a total preorder from a partial one, can be formalized by imposing constraints (9) to (11) – the coherence constraints for a total pre-order relation – on the preference functions (7).

---

2 Acronym for Preference Ranking Organisation METHod for Enrichment Evaluation.

3 Note that this method is still considered a referent in the study and verification of other methods of multicriteria analysis: see on this Leyva-Lopez and Fernandez-Gonzalez (2003).

By Dr Elvio Mattioli

Next: Outline of the PROMETHEE method

Summary: Index