As pointed out with regard to Table 1, the multicriteria preference indices defined in an additive scheme satisfy neither the reversibility (10) nor the transitive property defined for that scheme. However, it is of interest to find that the reversibility property is satisfied by multicriteria preference indices that measure the preference differential between the evaluations relative to symmetrical pairs of units. These are straightforwardly obtained from the indices (17) as follows:

dij = d(ai,aj) = sij – sji ; i,j = 1, …, n, (20)

or with matrix notation:

D = S – S’ (21)

The values assumed by these indices in the numerical example considered are set out in Table 4.

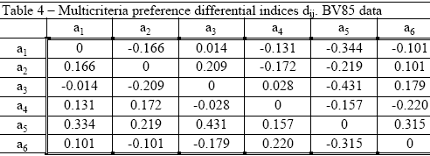
From this, violation of the transitive property is easily ascertained. For example

d13 = 0.014 ≠ d12+d23 = -0.166+0.209 = 0.043.

These indices are therefore incoherent for ranking the units and hence for constructing a total pre-order for them. This thus raises the problem of modifying them in order that they satisfy this property.

Moreover, because these indices result from empirical observations which take account of concrete needs both objective and subjective, the weights vi to associate with the individual units in order to satisfy relations (10) must be such as to make the smallest modifications possible to these multicriteria preference indices: in other words, there must be the minimum possible difference between the observed indices and those that are theoretically coherent. Formalizing this choice in the least squares criterion[6] entails the problem of minimizing the function:

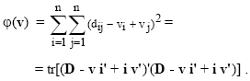(22)

The first-order conditions require:

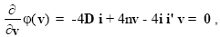(23)

whence:

(nI - i i') v = D i . (24)

It is evident that the (nI – i i’) matrix is singular,[7] which for that matter was to be expected given that the values vi have been determined up to an additive constant. If this is chosen so that the sum of the weights is annulled, i.e. i’ v = 0, one obtains the particular solution:

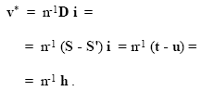(25)

This last relation justifies, I believe, the procedure for determining the scores to assign to the individual units foreseen by the PROMETHEE II to pass from the partial pre-order to the total one. In fact, scores (19) differ from weights (25) only for the multiplicative constant n-1, which is entirely without influence on the total pre-order of the units.

---

6 It should be also pointed out that, according to the same criterion, in the domain of skew symmetric matrices, which satisfy the less stringent constraint of reversibility, matrix D is to be preferred in that it minimises the norm S - D. I am grateful to an anonymous referee for this suggestion.

7 Suffice it to consider that (nI – i i’) i = 0.

By Dr Elvio Mattioli

Next: The alteration produced by the coherence constraints

Summary: Index