The approach proposed appears to be of especial interest because it enables evaluation of the divergences between the multicriteria preference indices observed and those closest to them in the sense of (22) but coherent with a total pre-order of the units. The practical and operational need for a ranking of the units that enables identification of those that should be regarded as preferable induces consideration of the partial pre-order, and therefore of the cases of non-comparability shown by the PROMETHEE I method, only as a negative aspect.

Instead, they yield useful information that can be profitably used by the decisionmaker to reconsider some of the choices previously made. The ranking yielded by PROMETHEE II does not furnish information of this type, nor does it indicate the extent to which the total pre-order obtained is realistic with respect to the actual preference indices observed.[8]

The procedure set out in the previous section enables one to address naturally and immediately the problem of evaluating the alteration introduced by the coherence constraints. In fact, for each pair of units, one need only consider the difference between the values of the preference differential indices dij and the corresponding values calculated using weights (25):

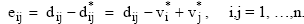(26)

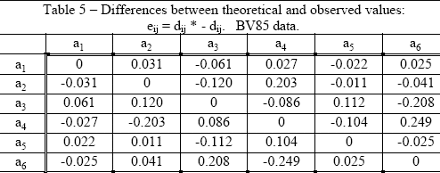
The values assumed by these (asymmetric) differences in the numerical example considered are shown in Table 5 below.

For the purpose of succinct analysis of the results of the procedure, I calculated the following indices:

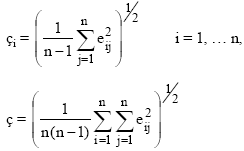(27) (28)

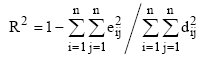(29)

which enable evaluation of the extent of the dissimilarity due to the individual units and the procedure as a whole, as shown in Table 6.

In order to further illustrate the usefulness of an objective measure of the difference between the partial and total pre-orders, I reconsidered the example provided in abovecited Brans, Vincke and Mareschal (1986, henceforth BVM86). It should be borne in mind that the diversity between the two orders is evaluated by these authors only by means of comparison between the two corresponding graphs shown in Figures 3 and 4.

I used indices (27), (28) and (29) to measure the dissimilarity between the two pre-orders quantitatively. The results are given in Tables 7 and 8.

The methodological approach proposed here also enables analysis to be made of the sensitivity of the complete final ranking to the choice of weights[9] πk, k=1,…,K, for the criteria Pk. By substituting relation (16) in (21) and (25), from (26) one obtains:

(30)

which makes it relatively simple to connect the measure of violation of the coherence constraints with evaluation of the importance assigned to the individual criteria.

---

8 This is an aspect also emphasised by the authors of the multicriteria decision-making method cited here, who already noted in their work of 1985 (Brans and Vincke, p. 656) that “PROMETHEE II provides a complete ranking which is ‘agreeable’ to the decision-maker, but some useful information about incomparabilities gets lost”. Brans, Vincke and Mareschal (1986, p. 234) provide a numerical example of the advantage of also considering and analysing a partial pre-order which highlights the misleading information that a complete pre-order may furnish, but without proposing measures of the diversities between the two rankings.

9 I am again grateful to an anonymous referee for this suggestion.

By Dr Elvio Mattioli

Next: Concluding comments

Summary: Index