Consider a large economy with a sufficiently large number of risky asset markets,
N. In each period t (t = 1, 2, . . .), the N risky assets’ returns, denoted by

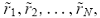are independently and identically distributed across markets. Each
asset market n (n = 1, 2, . . .,N) has two types of traders, denoted by i = 1, 2.

Type-1 traders are those who have correct beliefs about the distributions of risky
assets n in the market, whereas type-2 traders are those who misperceive the distributions of the risky asset due to cognitive errors (Kahneman et al. (1982)). In this sense, type-1 traders are rational and type-2 traders are nonrational. All traders are endowed with a constant capital c0 at the beginning of each period and may borrow or lend at a nonnegative riskfree rate r. In each period, individual type-i traders in asset market n choose their optimal demand qi;n for risky asset n to maximize their expected utility of the end-of-period wealth, given the current market price pn and their beliefs and information. At the end of the period, asset n’s return rn is realized and the type-i trader’s investment return, denoted by Ri,n, is given by

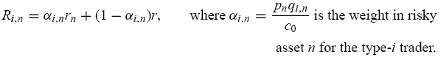(3)

The end-of-period wealth of type-i traders as a group is the sum of the realized
end-of-period wealth of all individual type-i traders across n markets. Let

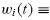
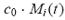be the wealth of type-i traders as a group at the beginning of period t.

The population share of the type-i traders as a group in period t, xi (t), is therefore determined by its wealth share at time t, xi (t) = wi (t)/(w1(t) = w2(t)), for i = 1,

2. This captures the notion that the more wealth a group has the more populous that group becomes. The distinction between wealth, wi (t), and population share, xi (t), is important because a group of traders can have positive wealth and yet become extinct in terms of its population share, when the group’s speed of accumulating wealth is of a lower order relative to the other group. In order to emphasize the dependence of individual traders’ returns on the population state, write Ri,n(x(t)) as the return of individual type-i traders in market n, given the current population
state x(t). Similarly, write 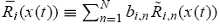as the average return of type-i traders across markets in period t, where the weight bi,n is the relative size of type-i traders in market n such that the weights across markets sum to one; i.e.,

=1.

1. In other words, the average return obtained by a given trader type
depends not only on the return he or she achieves in each market, ˜R i,n(x(t)), but also on his or her relative size in each of those markets, bi,n. The wealth of type-i traders as a group at the beginning of period t + 1 is
therefore given by

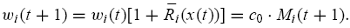(4)

Now, consider a “smooth” continuous-time counterpart of the above discretetime
wealth accumulation process such that at any fraction δ of the period, the
wealth of type-i traders as a group at time t + δ is given by

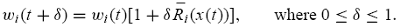(5)

Consequently, the population share of type-i traders as a group at time t + ± is
given by

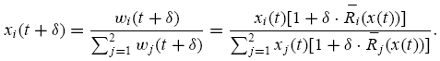
The instantaneous rate of the change in population share at time t, denoted by ˙xi (t), is obtained as follows:

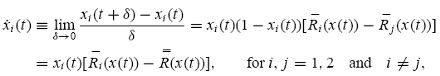
And

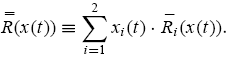
This dynamic indicates that the growth rate,

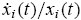
, of group i’s population share equals the difference between the group’s average return across all markets,

,

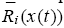and the population-share weighted average return of all traders in the
economy,

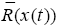
. This population dynamic emerges from the process of asset
accumulation and it shows that the investment return of different strategies (types) drives the evolutionary process in asset markets. When compared to the dynamic in (2), the dynamic in (7) indicates that the investment return of each strategy (type) is the strategy’s (type’s) payoff function for the population dynamic. Intuitively, this dynamic captures the spirit in real-world asset markets in the sense that the
rise and fall of investment funds depend on their relative return performance in the markets (Lakonishok et al. (1992)). This process is also consistent with the practice in real life in the sense that old investors die and new investors inherit money and the strategies of their parent investors. In general, the analysis of the stochastic process of the population dynamic in (7) is complex, because the average investment return of type-i traders, i.e.,

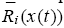
depends on individual type-i traders’ return in each market n, i.e.,

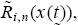
which is stochastic. However, if type-i traders’ size-adjusted returns, i.e.,

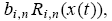
are independently distributed with finite variances across markets, then the average return of type-i traders across markets converges to the expected return of a representative type-i trader, denoted by

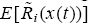
, as the number of markets, N,

becomes sufficiently large (see Shiryayev (1984, p. 364)). That is,

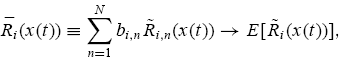
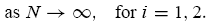
Since we consider an economy where the number of markets is sufficiently large and the risky assets’ returns are independently and identically distributed across markets, the above convergence result in (8) naturally holds in our model.We drop the subscript n in the RHS of (8), since the expectations are identical for all n. In such a large economy, the general population dynamic in (7) therefore becomes the following:

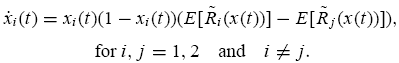
The population dynamic in (9) shows that in a large economy the instantaneous rate of change in the population share depends on the current expected return differential between the two types of traders, i.e.,

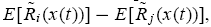
, which,in turn, depends on the current population state, x(t). In other words, the expected returns depend on the current population state and, at the same time, the change in the current population state depends on the expected returns. Such a dynamic relationship is important in real-world markets, because although higher expected returns tend to generate a greater population share, the greater population share
up to a certain level may hurt the expected returns in the future. Hence, it is important to determine simultaneously the population shares and the expected returns in a dynamic system as in (9). This is in contrast to the imitation process of DSSW (1990) where the returns are calculated under the assumption that the noise trader share is fixed. Moreover, our endogenously determined group wealth accumulation process distinguishes our population dynamic from other dynamics based on exogenously chosen individual imitation process as in DSSW (1990).

So far, we develop the population dynamic between rational and nonrational traders without specifying any particular kind of nonrational traders and show that their survival depends on the relative fitness as measured by their current expected return. In order to examine the survival of a particular kind of irrationality, one needs to model the trading game between the two types of traders and derive their corresponding payoffs, i.e., the expected returns, as a function of current
population state. This is what we turn to in the next two sections.

Section II examines the survival of overconfidence in a pairwise contest and Section III examines the survival of investor sentiment in a playing-the-field contest.

Prof. F. Albert Wang

Next: Overconfidence in a Pairwise Contest

Summary: Index