Degenerate PDEs of Kolmogorov type naturally arise in the problem of pricing path dependent contingent claims. The simplest significant example is given by Asian-style derivatives: if we assume that the stock price St is a log-normal stochastic process, i.e. a solution to the SDE (1.1) with µ, s fixed constants, then the price U of a geometric average Asian option is a solution to the equation

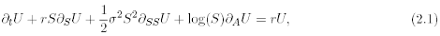
where “A” denotes the path-dependent variable and r is the risk-free rate (see, for instance, [25]). By an elementary change of variables, (2.1) can be reduced to the following PDE in R3

Although (2.2) is strongly degenerate due to the lack of diffusion in the x2-direction, Kolmogorov [16] constructed an explicit fundamental solution to (2.2) of Gaussian type, which is a C8 function outside the diagonal (cf. (2.11)). Consequently equation (2.2) has a closed form solution and is hypoelliptic, that is every distributional solution to (2.2) is a C8 function. As we shall see later, the Kolmogorov method can be applied in a very general framework. In the Hobson-Rogers model [14], the stock price St is described by an It process of the form

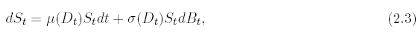
where Dt represents the deviation from the trend and is defined as the difference between the current value and a geometric, exponentially weighted average of past prices. More precisely, if

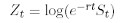
denotes the discounted log-price, then

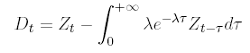
where ? is a positive parameter. Hobson and Rogers prove the existence of an equivalent probability measure under which the discounted price e ^-rt St is a martingale. Then usual no-arbitrage arguments can be used to determine derivative’s price.

In [14], it is proved that the price Ut of an European-style contingent claim with terminal payoff 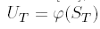is given by

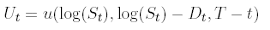
where

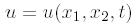
is the solution to the following degenerate PDE with variable coeffcients in R ³

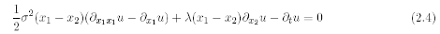
with initial datum

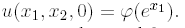
The same argument can be used for the more general case of a geometric average Asian option. Let At be the path-dependent process describing the geometric average of the underlying:

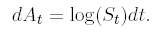
The price Ut of a derivative with terminal payoff

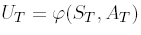
is then given by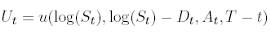

where 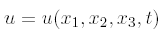is the solution to the PDE

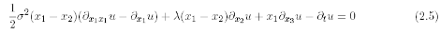
with initial datum

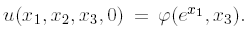
We emphasize that (2.5) is a PDE in R⁴ with diffusion only in the x1- direction.

The above examples motivate the study of the following class of degenerate PDEs.

Definition 2.1 We call Kolmogorov equation (in short, KE) a PDE of the form

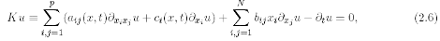
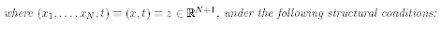
i) there exists µ > 0 such that

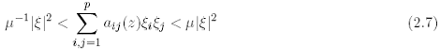
for every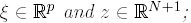

ii) the matrix B = (bij) is constant and has following block form

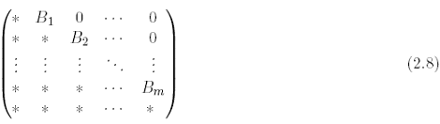
where the Bj’s blocks are pj-1 x pj matrices of rank pj , j = 1, 2,....,m, and the blocks denoted by * are arbitrary. Moreover the pj’s are positive integers such that

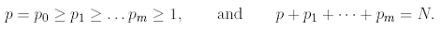
Example 2.2 Equation (2.2) is obviously a KE; in this case

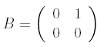
It is also clear that every parabolic equation is a KE.

To verify that equations (2.4) and (2.5) of the Hobson-Rogers model are KEs, it is convenient to recall that the structural assumptions of Definition 2.1 are equivalent to the well-known Hormander’s condition [15] (see, for instance, [18]). In our setting it reads: Hormander’s condition: the first order differential operators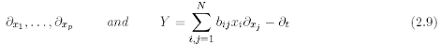

together with their commutators, span R^N+1 at every point.

Example 2.3 Equation (2.4) is a KE. Indeed, for every ? > 0, the first order differential operators

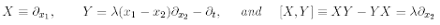
are linearly independent at every point and form a basis of R³. Analogously, equation (2.5) is a KE since

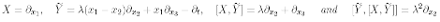
span R⁴ at every point.

Definition 2.4 A KE in the form (2.6) with constant

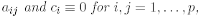is called a “Kolmogorov equation with constant coeffcients”.

The denomination “KE with constant coeffcients” stems from the theory of parabolic PDEs. Indeed a constant-coeffcients parabolic equation is nothing more that a translation-invariant equation on the Euclidean space. Similarly, a constant-coeffcients KE in the form (2.6) has the remarkable property of being invariant with respect to the non-Euclidean left translations in the law

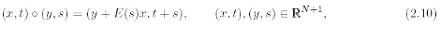
where E(t) = exp(-tBT ) and BT denotes the transpose of the matrix B.

In this case, the explicit expression of G (z; ? ), the fundamental solution of (2.6) evaluated in z with pole at ?, is given by G(z; ?) = G(?^-1 o z; 0) where

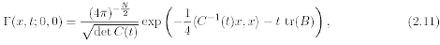
for (x, t) e R ^N x R⁺ and C(t) is the positive definite matrix

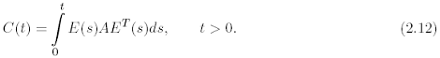
As usual, a solution to the Cauchy problem for (2.6) can be expressed in a closed form, as the convolution of the initial datum with the fundamental solution G. As in the classical theory, constant-coeffcients KEs serve as an essential class of prototypes and many results can be extended to the general situation of variable coeffcients by perturbation arguments (see, for instance, the survey [17]). Among constant-coeffcients KEs, a particularly important role is played by equations for which all the *-blocks in (2.8) are zero matrices. Indeed these KEs has the remarkable property of being homogeneous with respect to the dilations ( d ? ) ? >0 in R ^N+1 defined by

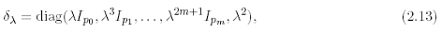
where Ipj denotes the pj x pj identity matrix. More precisely, it holds

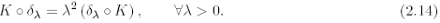
For example, equation (2.2) is homogeneous with respect to the dilations

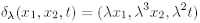
On the contrary, in the KEs arising in the Hobson-Rogers model not all the *-blocks are null. The main result of this section is the following theorem proved in [19] (see also [22] for the case of null *-blocks). In the next statement,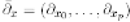 denotes the gradient in the first p variables, Yz, Y? respectively denote the first order differential operators in (2.9) acting on the variables z = (x, t) and ? = (y, s). Moreover we say that a function f is slowing increasing if

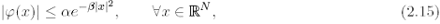
for some positive constants a , ß.

Theorem 2.5 Assume that the coeffcients of the KE (2.6) are infinitely differentiable in R^Nx]0, T[ and that all the derivatives are bounded functions. Then (2.6) has a fundamental solution G: in particular, for everyf e C(R^N), slowly increasing with suitably small ß in (2.15), the function

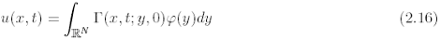
is the unique slowly increasing, classical solution to the Cauchy problem

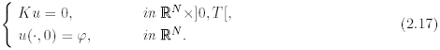
Moreover the function ¡(z; ?) is infinitely differentiable for z ? ? and we have the following estimates of the derivatives:

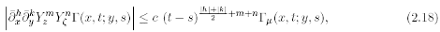
where G µ is the fundamental solution of the constant-coeffcients KE with (aij) = µ Ip and µ as in (2.7). The explicit expression of G µ is given in (2.11). The constant c depends on the multi-indexes h, k and on the non-negative integers m, n.

Remark 2.6 The hypotheses on the regularity of the coeffcients in the previous statement can be considerably relaxed. For the existence of G, it is suffcient to assume that the coeffcients are bounded and Holder continuous. Analogously, estimate (2.18) still holds true under usual hypotheses: the regularity of order k + a , a > 0, of the coe±cients implies an estimate of the derivatives of order k + 2 of G. Note that Y has to be considered as a second order derivative.

M. Di Francesco, A. Pascucci www.dm.unibo.it/~pascucci

Next: A numerical scheme

Summary: Index