L'insieme di Cantor
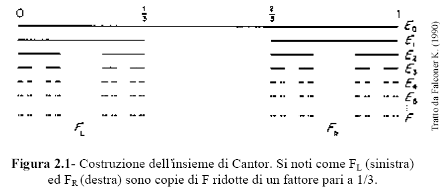
L'insieme di Cantor è uno dei più semplici oggetti frattali cui si possa far riferimento. Nonostante la sua semplicità, presenta le tipiche caratteristiche degli oggetti frattali. Esso è costruito partendo da un segmento di lunghezza unitaria cui sono iterativamente eliminati alcuni tratti (figura 2.1).
Sia E0 l'intervallo [0,1]. Sia E1 il set ottenuto togliendo dal centro del segmento E0 un segmento di lunghezza 1/3, cosicché E1 sia composto dai due intervalli [0, 1/3] e [2/3, 1].
Ripetendo la stessa operazione con questi due intervalli si ottiene il set E2 composto dagli intervalli [0,1/9], [2/9, 1/3], [2/3, 7/9], [8/9, 1]. In generale Ek è ottenuto togliendo la parte centrale di lunghezza 1/3 del segmento Ek-1; dunque Ek è formato da 2k intervalli ciascuno di lunghezza pari a 3-k. Il set F è ottenuto dall'intersezione di tutti gli Ek:
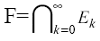
F è il limite della sequenza Ek per K che tende all'infinito. Si noti che alcuni punti non vengono mai rimossi durante il processo, benché la retta iniziale di lunghezza unitaria venga rimossa completamente; infatti, ricordando come l'insieme è costruito, la somma totale dei segmenti eliminati è pari a:
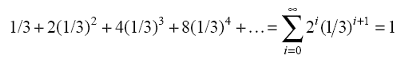 (2.1)
(2.1)
L'insieme di Cantor non è vuoto ed è composto da un numero infinito di punti. Infatti, eliminando il terzo centrale da ogni segmento, ad ogni iterazione si ottengono dei segmenti che sono di lunghezza totale pari a 2/3 del segmento precedente. Quindi (2/3)n del segmento unitario di partenza alla n-esima interazione. Per n che --> ∞, (2/3)n -->0.
Ogni estremo di un intervallo rimosso appartiene all'insieme, in quanto a ogni stadio successivo è rimosso un intervallo adiacente, ma che non contiene questo estremo. Ne segue che i punti 0, 1, 1/3, 2/3, 1/9, 2/9, 7/9, 8/9, ecc., appartengono tutti all'insieme di Cantor. Inoltre l'insieme non contiene intervalli: se ne contenesse, infatti, in qualche passaggio ne sarebbe stato rimosso il terzo centrale finché non fossero rimasti che punti isolati. Ciò significa che l'insieme è totalmente non connesso: tra due suoi qualsiasi punti devono esistere dei punti che non appartengono all'insieme.
Da questo noto oggetto frattale si possono desumere già alcune caratteristiche presenti anche in altri frattali.
1) F è autosomigliante. Le parti di F nell'intervallo [0, 1/3] e quelle nell'intervallo [2/3, 1] sono geometricamente simili a F, ridotte di un fattore pari ad 1/3. Gli elementi di F, in ciascuno dei quattro intervalli di E2, sono simili a F ridotti di un fattore pari a 1/9, e così via. L'insieme di Cantor contiene copie di se stesso ridotte per un fattore di scala qualunque sia la scala di riferimento.
2) F ha una struttura "fine". Per quanto ridotta sia la scala di osservazione il dettaglio dell'immagine non viene meno.
3) F è ottenuto per mezzo di una procedura ricorsiva. Nel caso in esame tale procedura consiste nell'eliminazione reiterata del terzo centrale di ciascun nuovo segmento. Ogni iterazione porta ad una migliore approssimazione Ek di F.
4) La geometria di F non è facilmente descrivibile in termini di geometria classica. Non è il luogo dei punti che soddisfano qualche semplice condizione geometrica, né l'insieme delle soluzioni di un'equazione.
5) La descrizione della geometria locale di F non è semplice; vicino a ciascun punto esistono infiniti altri punti separati da spazi vuoti, che non appartengono all'insieme, di varie lunghezze.
La curva di von Kock, il triangolo di Sierpinski e gli insiemi di Julia
Un altro frattale storicamente importante è quello immaginato dal matematico Helge von Kock nel 1904 (figura 2.2). Sia E0 un segmento di lunghezza unitaria. Il set E1 è composto da quattro segmenti ottenuti rimuovendo il tratto centrale di lunghezza 1/3 dal segmento E0 e sostituendo la parte liberata con i due lati di un triangolo equilatero senza la base. La stessa procedura è applicata a ciascuno dei quattro segmenti di E2 ottenendo il set E3. In generale Ek è ottenuto sostituendo la parte centrale di lunghezza 1/3 di ogni segmento di Ek-1 con i due lati di un triangolo equilatero senza la base. Quando k è relativamente grande le curve Ek-1 ed Ek differiscono solo per brevilinee particolarità e per k che tende ad infinito, la sequenza del poligono Ek approssima la curva limite F chiamata Curva di von Kock.
Le caratteristiche della curva di Kock sono simili a quelle elencate nel caso
dell'insieme di Cantor. Ciascun tratto, singolarmente considerato, è somigliante all'intera
curva, ma ridotta di dimensione per un fattore pari a 1/3 rispetto al predecessore. La struttura
"fine" dell'oggetto è evidenziata dalle frastagliature visibili ad ogni scala. Ciononostante,
l'intricata struttura emerge da una semplice regola di costruzione. 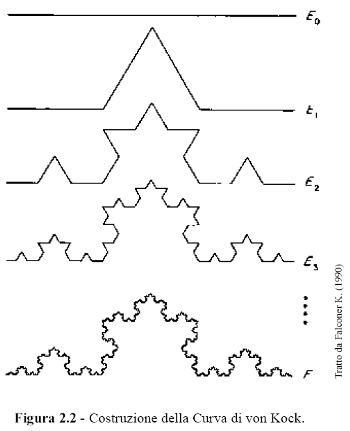
La lunghezza di Ek si dimostra essere uguale a (4/3)k; dunque per N che tende ad infinito, F ha una lunghezza infinita. Tutto ciò è abbastanza in contrasto con le usuali forme geometriche, come le linee spezzate, che hanno una lunghezza finita. Sono molti gli oggetti frattali che possono essere generati usando una regola ricorsiva. Un altro esempio è il triangolo di Sierpinski ottenuto partendo da un triangolo equilatero solido. Ad ogni iterazione si rimuove (invertito) un triangolo equilatero nella parte centrale di ogni triangolo solido che compone l'intera figura (figura 2.3). Questo triangolo non contiene regioni bidimensionali: ogni parte piena del triangolo originale è "forata" dalla rimozione di altri piccoli triangoli.
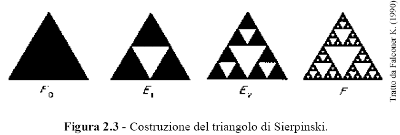
Per capire in che cosa consiste l’autosomiglianza in quest’oggetto, si noti innanzi tutto che il lato ci ciascun triangolo è esattamente la metà di quello precedente. Ingrandendo uno solo dei triangoli che compongono la figura vedremmo che esso è esattamente uguale alla figura intera. Indipendentemente dalla profondità alla quale lo si guarda, la porzione del triangolo del livello n del processo di iterazione darà esattamente, se ingrandita di un fattore 2n, una copia dell'intero triangolo.
Le leggi che queste immagini descrivono sono idealizzazioni. Nessuna struttura reale, ad esempio, può essere ingrandita infinite volte rimanendo uguale a se stessa. Una sorta di omotetia interna [1] si realizza approssimativamente nelle forme naturali. I meccanismi che generano tali strutture sono descrivibili, invece che con regole di iterazione grafica, con semplici iterazioni del tipo rappresentato in figura 2.4 basate su una qualche funzione matematica f.
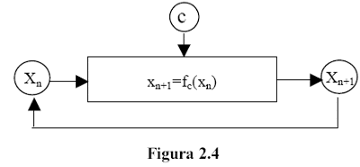
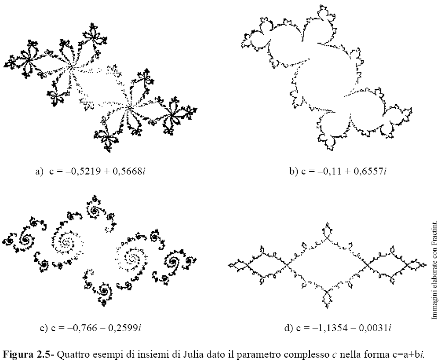
Di volta in volta, il dato in uscita diventa dato d'ingresso per l'operazione successiva. La correlazione tra input e output sarà non lineare, ossia la legge dinamica Xn+1=fc(Xn) non potrà ridursi ad una semplice proporzionalità diretta. Un esempio classico è la funzione xn+1=xn2+c che, opportunamente implementata in un algoritmo iterativo, è in grado di generare le immagine di figura 2.5 per un opportuno valore di della costante complessa c. Si tratta dei cosiddetti insiemi di Julia. Il comportamento della successione Xn dipende solo dalla costante c e dal punto iniziale X0 variato nel piano complesso.
Si può pensare al processo di iterazione definito dalla formula richiamata come a un modo per rendere esplicita l'informazione contenuta nei dati (in questo caso solo quella contenuta nel parametro c). Offre un esempio di come un sistema dinamico molto semplice possa sviluppare la poca informazione contenuta nei dati iniziali producendo varie strutture altamente organizzate. Benché tali strutture non siano perfettamente autosomiglianti nel senso visto dell'insieme di Cantor o della curva di Kock, le singole parti dell'intera figura sono però "quasi autosomiglianti" o "autosimili" nel senso che una porzione dell'intero oggetto può essere ingrandita mantenendo comunque una forma che ha una struttura di base qualitativamente simile a quella del tutto.
Giancarlo Fabbro
Successivo: Alcuni esempi di oggetti frattali II
Sommario: Indice