
Il problema della definizione del valore di mercato di una qualsivoglia azienda fu affrontato in maniera sistematica per la prima volta da Sir John Burr Williams, il quale nel suo “The Theory of Investment Value” del 1938 elaborò un sistema per l’epoca rivoluzionario. Williams introdusse per la prima volta l’idea che il valore di un’azienda dovesse essere calcolato sulla base dei dividendi attesi in futuro.
Egli, inoltre, ben conscio delle difficoltà di stima dei dividendi futuri e, soprattutto, del tasso di incremento degli stessi, arrivò ad ipotizzare dei modelli con differenti tassi di crescita.
Sebbene con Williams si ebbero dei notevoli passi in avanti verso un efficiente modello di valutazione degli investimenti, occorrerà attendere la pubblicazione, nel 1956, di un articolo a cura di Gordon e Shapiro “Capital Equipment Analysis: the Required Rate of Profit” e la successiva “sistematizzazione” della teoria ad opera di Gordon nell’articolo “The Investing, Financing and Valuation of the Corporation” del 1962 per poter parlare di un vero e proprio “Modello dei Dividendi Scontati”.
Il Dividend Discount Model (DDM) è anche noto, in lingua italiana, come “Modello a Crescita Costante”: ciò in quanto il prezzo di una attività finanziaria è ottenuto come somma dei flussi dei dividendi futuri attualizzati ad un tasso di sconto costante.
Il valore attuale del flusso dei dividendi attesi può essere espresso come:
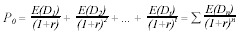
dove:
P0 = prezzo corrente dell’azione
E(Dt) = dividendo atteso per l’anno t
n = numero degli anni di attività dell’impresa
r = tasso di attualizzazione aggiustato per il rischio.
Questa equazione ipotizza che l’investitore detenga il titolo per tutta la durata della vita dell’azienda. Essendo tale ipotesi assai irrealistica il modello prevede che il valore del titolo possa venir calcolato anche nel caso in cui il titolo sia detenuto per periodi inferiori. Se, ad esempio, il titolo è detenuto per due anni il prezzo sarà calcolato come:
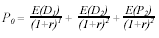
dove:
E(P2) = prezzo atteso alla fine del secondo anno.
Ad una prima lettura si potrebbe obiettare che il prezzo dell’azione non sembra essere spiegato dai dividendi attesi. In realtà è possibile dimostrare che la (2) sia uguale alla (1): basterà supporre che un ipotetico investitore, alla fine del secondo anno, offra un prezzo basato su i dividendi futuri ( D3, D4,…) e che le aspettative sui dividendi e sul tasso di sconto siano uguali a quelle precedenti. Il prezzo atteso dopo il secondo anno sarà:
Sostituendo questo valore all’E(P2) nell’equazione (1), avremo:

che è uguale alla (1).
E’ possibile concludere, quindi, che tutti gli investitori si preoccupano solamente del prezzo di acquisto, dei dividendi ricevuti durante il periodo di detenzione del titolo e del prezzo di vendita. L’equazione (1) stima tutti i dividendi pagati nella vita dell’azienda: in realtà quanto visto finora è solo una “introduzione” al modello di Gordon vero e proprio.
Il Dividend Discount Model assume tre ipotesi di base:
1. il flusso dei dividendi è perpetuo
2. i dividendi crescono sempre ad un tasso costante g
3. il tasso di sconto è maggiore del tasso di crescita (r > g)
Partendo dalle prime due ipotesi l’equazione (1) diverrà:
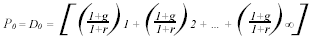
Si tratta di una equazione in forma geometrica, in cui il fattore geometrico è (1 + g)/(1 + r). Ricostruendo la (4) secondo la progressione geometrica, otterremo:
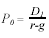
E facile notare come D1 sia uguale a D0(1 + g): quest’ultima equazione rappresenta “il succo” del modello di Gordon.
Sebbene l’ipotesi di un tasso costante nel tempo risulti alquanto forte, l’equazione si pone come un ottimo strumento per analizzare le principali determinanti dei prezzi e dei rendimenti. L’equazione (5) può essere riscritta come:
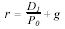
Si può quindi concludere che il rendimento complessivo può essere scomposto in due componenti, il tasso di dividendo D1/P0 e il tasso di crescita g: se il tasso di capitalizzazione, r, è costante, la crescita del prezzo dell’azione sarà uguale al tasso di crescita dei dividendi.
Dott. Andrea Castiglione
Successivo: Franco Modigliani Merton Miller
Sommario: Indice