Nelle applicazioni finanziarie, l’ordine dei dati, segnato dalle date, se si stanno trattando dati giornalieri, oppure dalla data e l’orario, se si considerano dati intraday, è un fattore rilevante che i modelli predittivi dovrebbero tener presente. La dimensione tempo, dunque, introduce un altro livello di complessità nell’analisi e fa riaffiorare alcune domande: quali punti del learning set vanno a stimare ciascun punto del test set? Quanta importanza si deve dare ai records più recenti e quanta a quelli più datati? E quando un records si può dire che è datato?
Quando si trattano serie storiche, la dimensione temporale è importante, in particolar modo, quando si modellano dati finanziari è ragionevole assumere che i records più recenti siano maggiormente rilevanti rispetto ai dati di un periodo antecedente. Se bisogna prevedere il valore di y in un dato momento temporale si devono considerare maggiormente i learning points più vicini a quel periodo, è assurdo, infatti, ottenere dei buoni modelli predittivi se le stime dei valori vengono basate equamente su punti datati e punti recenti del learning set.
Un semplice criterio per dare più importanza ai punti più attuali è quello di pesare i dati in base al tempo, così facendo il kernel esponenziale (eq. 2.2.2) deve essere modificato in questo modo:
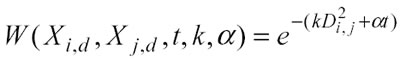
In questa equazione t è la differenza temporale tra il tempo associato al jesimo punto di test e l’i-esimo learning point, α è una costante temporale definita dall’analista in base alla percezione soggettiva che ha sul peso dato dalla variabile tempo: se il tempo viene misurato in unità di un giorno e l’analista ritiene che le informazioni apprese da dati vecchi di un anno (365 giorni) debbano ricevere metà del peso delle informazioni correnti, allora α sarà calcolato risolvendo l’equazione:
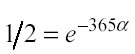
da cui
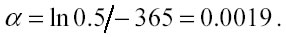
Successivo: 4.1 Presentazione della Matrice dei dati
Sommario: Index